Mathe Aufgabe?
Kann mir jemand bei dieser Aufgabe helfen. Verstehe leider nicht wie ich das rechnen soll.
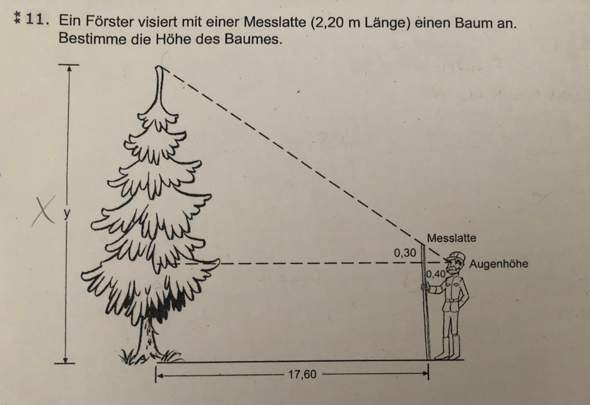
danke im voraus
5 Antworten
Mit einem Strahlensatz kannst du das berechnen
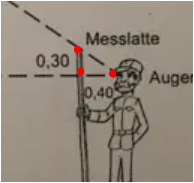
Hey, das ist eine spezielle Anwendung der Strahlensätze und wird Försterdreieck genannt. Wenn der Förster die Messlatte gerade hält und genau auf die Spitze des Baumes schaut, dann ist seine Entfernung zum Baum genau die gleiche Länge, wie die gegenüberliegende Seite des großen Dreiecks. Allerdings muss man zusätzlich noch die Augenhöhe beachten. Also erstmal aufschreiben was wir alles haben: Die Entfernung des Försters zum Baum beträgt 17,60m + 0,40m = 18m. Dann ist die gegenüberliegende Seite des großen Dreieck auch 18m lang. Jetzt fehlt aber noch die seine Augenhöhe, die wir dazu addieren müssen. Seine Augenhöhe die Höhe der Messlatte (2,20m) minus die 0,30m der gegenüberliegenden Seite des kleinen Dreiecks, Also 2,20m - 0,30m = 1,90m. Dann ist die Höhe des Baumes y = 18m (Entfernung zum Baum) + 1,90m (Augenhöhe). Die Höhe des Baumes beträgt dementsprechend 19,90m.
Ergebnis kann nicht stimmen, ist auch kein Försterdreieck, da nicht gleichschenklig
Das ist einfacher Strahlen- und Dreisatz.
Sieht halt nur komisch auf dem Bild aus.
In Formeln:
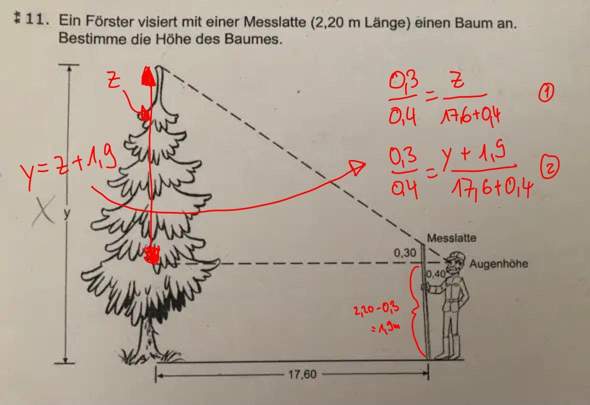
Idee
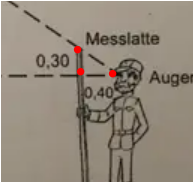
dieses kleine Dreieck ist starkvergrößert worden , Statt 0.40 nun (17.60+0.40)=18 , statt 0.30 nun die noch unbekannte Teilhöhe H der Tanne : 0.3/0.4 = H/18.00 (***).........H über 13 Meter
Nun noch 2.20 - 0.30 dazurechnen . Warum ?
.
::
(***) hier wurde korrigiert .
Genau genommen H / (17,60 + 0,40)
Wobei, vielleicht wird das in der Praxis sogar vernachlässigt, da sich das Ergebnis dadurch nicht viel unterscheidet
genau kann es bei Mathe schon mal nehmen . 13.2 zu 13.5 ist ja schon ein Unterschiede . Wobei mein alter , jetzt korrigierter , Wert mit 13.20 die Tanne mangels ausreichender Höhe vielleicht noch vor dem Schicksal des Weihnachtsbaumes gerettet hätte.
Verwende das Konzept der ähnlichen Dreiecke: das Verhältnis zweier Seiten in ähnlichen Dreiecken ist gleich
(y-2.2+0.3) / (17.6+0.4) = 0.3/0.4
Stelle nun die Gleichung nach der Baumhöhe y um
2) kann nicht stimmen