Lenkung mit der Geschwindigkeit kombinieren?
Hallöchen,
ich hätte da eine kleine Frage an euch. Ich programmiere nebenbei und habe eine mathematische Formel aufgestellt wo ich nicht ganz weiterkomme.
Es geht darum, dass ich ein Lenkrad habe mit dem ich -90 bis 90 Lenken kann. Diese soll mit der Kombination der Geschwindigkeit die XY achse eines Fahrzeugs angeben. Leider habe ich irgendwie einen Denkfehler und würde mich um eure Hilfe freuen.
Der Lenkwinkel für die X Y wird berechnet indem man:
X =cos(Lenkwinkel)
Y=sin(Lenkwinkel)
Dazu multipliziere ich einfach die Geschwindigkeit
Also x * gesw und y * gesw für meine Koordinaten.
Weißt jemand wo der Fehler liegt bzw. wie ich es besser machen könnte?
3 Antworten
Was soll x und y sein und in welchem Koordinatensystem soll das sein.
Im Koordinatensystem des Fahrzeugs zeigt der Geschwindigkeitsvektor immer in Fahrtrichtung bei der Kurvenfahrt sorgt eine Kraft auf die Seite nur dafür dass er sich kontinuierlich weiter dreht.
Was willst du den überhaupt als Ergbenis deiner Rechnung am Ende haben? Wenn du die Bewegung des Fahrzeugs berechnen willst musst du die Bewegungsdiffgleichungen aufstellen und die lösen.
Ja aber welcher Koordinatensystem?
Ein Ruhesystem ein mitbewegtes Koordinatensystem oder was soll das genau sein?
Wenn du ein Fahrzeug simulieren möchtest musst du dir die Bewegungsgleichungen bilden und diese Differentialgleichungen lösen oder diese auf Differenzengleichungen umschreiben und durchiterieren.
Im wesentlichen geht das am einfachsten dass du die Bewegungsgleichungen zunächst im Koordinatensystem des Fahrzeugs aufstellst und dann auf dein Koordinatensystem rücktransformierst.
Die haben dann hald für die Geradlinige Bewegung die Form
pk+1 = pk + v*deltat
pk+1 ist dabei die neue Position des Fahrzeugs nach deltat sekunden und pk ist die vorherige Position.
Diese Differenzengleichungen kannst du direkt im Programm auswerten.
Oder anders gesagz willst du einen Punkt am Bildschirm sich bewegen lassen und die Bewegungen von diesem ändern?
Oder willst du eine Physikalische Simulation eines Fahrzeugs oder willst du ein Rennspiel nach programmieren oder was ist dein generelles Ziel?
Ich danke dir schonmal für deinen Versuch mir zu helfen.
ich habe ein Programm mit dem ich die verschiedenen Einschlagswinkel eingebe und diese werden mit der Geschwindigkeit kombiniert. Am ende wollte ich auf dem Koordinatensystem den Weg des Autos sehen.
Ich will ein einfaches Spiel entwickeln, wobei die Autos von dem Spieler kontrolliert werden. Diese fahren nach rechts oder links, je nach Lenkung. Aber mir reicht es Anfangs, wenn ich auf dem Koordinatensystem die Strecke des Fahrzeugs sehe.
So wie ich es verstehe ist bei dir v*(delta) die Geschwindigkeit abhängig von der Zeit?
Um also die Position immer wieder neu zu errechnen müsste ich:
X: pk+1 = pk + v(konst) * cos(winkeleinschlag)
Y: pk+1 = pk + v(konst) * sin(winkeleinschlag)
Falls ich es falsch habe oder nicht richtig verstanden habe, bitte ich um entschuldigung
Ja so in etwa.
Aber du tust dir einfacher wenn du den Ansatz mal etwas anders machst. Ich schreib das mal mehr oder weniger als Objektorientiertes Programm an.
class DrawingObject
int xposition;
int yposition;
double drehwinkel;
abstract DoIteration();
Dieses Objekt repräsentiert jetzt dein Fahrzeug in der Bildschirmebene. Es hat eine Position und einen Winkel in dem es steht.
Es hat außerdem die Funktion DoIteration die einen Berechnungsschritt darstellt.
Jetzt hast du dein Fahrzeug
class Fahrzeug extends DrawingObject
DoIteration()
int deltax = v*cos(Lenkeinschlag)*timediff
int deltay = v*sin(Lenkeinschlag)*timediff
In der Klasse Fahrzeug befinden wir uns im Kooridnatensystem des Fahrzeugs an sich. Sprich wenn wir einen Lenkeinschlag von 0 haben bewegen wir uns nur einen Schritt in die x Richtung unseres Fahrzeugs.
Jetzt müssen wir eine sogenannte Galileo Transformation machen. Für diese müssen wir den Vektor aus deltax und deltay zunächst um den drehwinkel genannten Winkel im Objekt drehen und dann eine Vektoraddition machen und zuletzt noch den Winkel anpassen.
Also geben wir dem DrawinObjekt die Methode
TransformAndUpdate(x, y)
xposition = x*cos(drehwinkel);
yposition = y*sin(drehwinkel);
drehwinkel = drehwinkel + arctan(y/x);
Das was wir hier machen ist wir drehen den Vektor aus dem Coordinatensystem des Fahrzeugs in unser Bildschirmkooridnatensystem und berechnen die neue Position auf der Zeichenfläche. Am Ende drehen wir das Objekt weiter, denn logischerweise steht das Auto nach dem Lenken mit einem anderen Winkel auf der Zeicheneben.
Mit arctan(y/x) berechnen wir den Winkel des Geschwindigkeitsvektors des Fahrzeugs. Allerdings musst du achten, dass wenn das Fahrzeug im 90° Winkel abbiegt, also x = 0 ist da eine Division durch 0 steht. Du musst diesen Fall also gesondert behandeln. Schreib dir dazu am besten eine Hilfsfunktion um den Winkel eines Vektors zu berechnen.
Btw der Code soll dir nur mal einen Anhaltspunkt liefern, ich kann nicht garantieren dass ich mich nicht irgendwo vertan habe, aber das ist imho die einfachste Möglichkeit wie du diese Dinge machen kannst.
Du hast durch die Trennung von Fahreugkoordinatensystem zu Zeichenebene auch die Möglichkeit grundlegende Physik wie Trägheit einfach zu implementieren.
Btw du solltest den Drehwinkel auch auf maximum 360° beschränken und die Winkel die nach drehwinkel + arctan... rauskommen aufs Intervall [0-360°] rückrechnen. Außerdem musst du drauf achten, dass die Winkelfunktionen in den meisten Sprachen mit Radiant rechnen und nicht in Grad.
Mir ist gerade aufgefallen, dass die Vector Drehung bei TransformAndUpdate nicht passt.
Der Vector muss mit der Drehmatrix gedreht werden.
Also
xposition = x*cos(drehwinkel) - y*sin(drehwinkel);
yposition = x*cos(drehwinkel) + y*sin(drehwinkel);
Ich hab auch ein kleines C# Programm geschrieben wo ich so ein Rechteck auf dem Bildschirm hin und herfahren lasse. Das kann ich dir gerne zukommen lassen wenn du möchtest.
Hi sugarww!
Ich finde, dein Denkansatz geht in die richtige Richtung. Ich tu mir gerade nur noch ein wenig schwer damit genau zu verstehen, was dein gewünschter Output ist. Die Geschwindigkeit gibt an, wie schnell sich die Position ändert (Strecke pro Zeit). Hier ist die Strecke im Prinzip die Differenz von X0 zu X1 (bzw. Y0 zu Y1).
X und Y sind aber statische Koordinaten. Geht es quasi um "delta X" und "delta Y"? Falls ja, ist das auf eine bestimmte Zeit genormt, also "delta X pro Sekunde" bzw. "delta Y pro Sekunde"?
X und Y sollen die Achsen des Koordinatensystems sein. Außerdem soll das Koordinatensystem die Position des Fahrzeuges anzeigen.
Ja, ich bitte um Entschuldigung für die undeutliche Erklärung. Ich habe ein Programm mit dem ich verschiedene Einschlagswinkel eingebe und diese werden mit der Geschwindigkeit kombiniert. Am ende wollte ich auf dem Koordinatensystem den Weg des Autos sehen.
Ok, ich interpretiere einfach mal die Geschwindigkeit als deltaX bzw. deltaY pro Zeiteinheit. Angenommen deine Koordinaten sind die Distanz in Metern, dann könnte dein Koordinatensystem ganz normal "m/s" verarbeiten.
In dem Fall hast du aus meiner Sicht alles richtig gemacht. Die Veränderung der Position als Ausdruck von X und Y (delta X als Änderung der Position in X-Richtung und delta Y als Änderung der Position in Y-Richtung) entspricht
dX = sin(Lenkwinkel)
dY = cos(Lenkwinkel)
Die neuen Koordinaten sind also
X = X0 + dX
Y = Y0 + dY
Ich habe ein Beispiel mit einer Geschwindigkeit von 6 m/s gemacht unter der Prämisse, dass die X- und Y-Koordinaten ebenfalls in Metern angegeben werden.

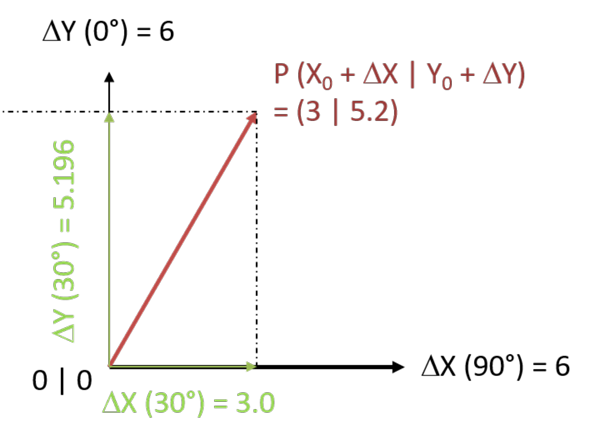
X und Y sollen die Achsen des Koordinatensystems sein. Außerdem soll das Koordinatensystem die Position des Fahrzeuges anzeigen