Konvergenz einer Funktion bildlich vorstellen?
Hallo allerseits. Ich habe momentan Probleme damit, mir bildlich vorzustellen, was es bedeutet, dass eine Funktion konvergent ist.
Bei der Konvergenz von Folgen habe ich verstanden, wie das grafisch aussehen kann. Hier könnte man ja z.B. einen Zahlenstrahl zur Veranschaulichung nehmen. Wenn die Folge dann z.B. gegen a konvergent ist, dann liegen in einer Epsilon-Umgebung von a fast alle Folgenglieder.
Bei der Konvergenz von Funktion habe ich nun Schwierigkeiten. Um eine Funktion grafisch darzustellen würde ich zunächst ein zweidimensionales Koordinatensystem wählen. Was ich nun nicht verstehe, ist, wie sich die Konvergenz einer Folge (z.B. im Punkt a) auf den Graph der Funktion auswirkt.
Ich habe zunächst versucht, mir mit der Definition der Konvergenz einer Funktion zu helfen. Demnach muss es nun einen Häufingspunkt (nennen wir ihn a) der Definitionsmenge (nennen wir sie D) geben. Damit die Funktion (nennen wir sie f) nun konvergent ist, muss für alle Folgen (nennen wir diese (x_n)) von Elementen aus D ohne a, die gegen a konvergieren, gelten, dass auch die Folgen (f(x_n)) konvergent sind.
Das erste, das mich verwirrt, ist, dass die Folgen (f(x_n)) nicht gegen ein bestimmten Wert konvergent sein müssen (vgl. Stetigkeit) sondern nur irgendwie konvergieren müssen. Ich habe zwar erfahren, dass diese Folgen dann, wenn f in a tatsächlich konvergent ist, gegen denselben Grenzwert konvergieren, was für ein Wert das dann aber ist, bleibt offen.
Auch habe ich herausfinden können, dass es immer eine Folge in D ohne a gibt, die gegen a konvergiert, beispielsweise (a - 1/n) oder (a + 1/n). Eine der beiden Folgen muss ab einem ausreichend großen n Element der natürlichen Zahlen in D liegen, falls D kein einzelner Punkt ist. Das wirft bei mir aber ganz nebenbei die Frage auf, was passiert, wenn D aus nur einem Punkt besteht als D=[x;x] ist.
Irgendwie habe ich mich festgefahren und komme nicht mehr weiter. Wenn mir also jemand dabei helfen könnte, diesen Sachverhalt zu visualisieren, wäre ich sehr dankbar!
3 Antworten
Hier
https://www.spektrum.de/lexikon/mathematik/gleichmaessige-konvergenz/4819
findest du nicht nur eine recht anschauliche, sondern auch mathematisch fundierte Erläuterung mit dem zentralen Bild des "Epsilon-Schlauches" um die Grenzfunktion herum, ebenso einige Beispiele von nicht gleichmäßig konvergenten Funktionenfolgen, also solchen die nicht in den Schlauch passen.
Nachtrag: Im Buch von Heuser: Lehrbuch der Analysis I findest du im Kapitel XIII Vertauschung von Grenzübergängen. Gleichmäßige und monotone Konvergenz weitere nützliche Beispiele und Bilder.
Deine letzten beiden Abschnitte habe ich nicht verstanden.
Eigentlich ganz einfach: Bei der "Konvergenz" einer Funktion (ein unüblicher Ausdruck) meint man, ob die Funktion einem endlichen GRENZWERT (limes) zustrebt oder nicht.
Beispiel: f(x)=x/(x+1) strebt für x gegen unendlich gegen den Wert 1.....geht also immer dichter an "1" heran, ohne sie für endliche x-werte exakt zu erreichen.
Anderes Gegen-Beispiel: f(x)=e^x.
Hier wird f(x) immer größer bei wachsendem x ----konvergiert also nicht.
Das ist z.B. ganz gut hier erklärt: https://de.wikipedia.org/wiki/Grenzwert_(Funktion)
Vielleicht verstehst du es so.
Achtung : Der Grenzwert muss im Allgemeinen nicht mit dem Funktionswert übereinstimmen (dann wäre sie stetig). Das Bild soll nur den Sachverhalt von der Definition besser erklären.
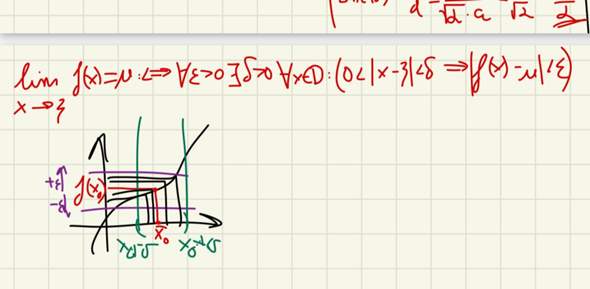
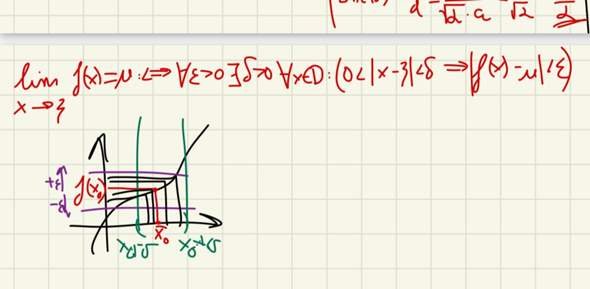
Danke für deine Antwort. Wenn x gegen (minus) unendlich geht, verstehe ich das.
Mein Problem ist, was passiert, wenn x gegen eine reelle Zahl geht. Irgendwie schaffe ich es nicht, dass zu übertragen.