Kondensator RC schaltung PHI berechnen?
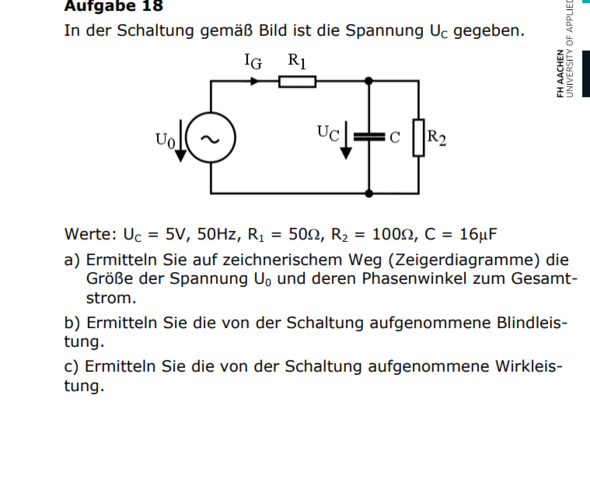
Wie kann ich bei folgender Aufgabe das Phi berechnen?
Formeln sind mir bekannt, aber die vorgehensweise nicht. Ich brauche das Phi um die Blindleistung und Scheinleistung zu berechnen.
6 Antworten
Anbei die ausführliche Berechnung des komplexen Scheinwiderstandes


Danke für deine ausführliche Lösung. Ich habe erst Xc komplex ausgerechnet und dann erst in die Formel eingesetzt. Und klappte wunderbar dank deiner Hilfestellung.
Betrag des komplexen Scheinwiderstandes Z
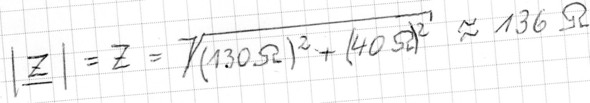
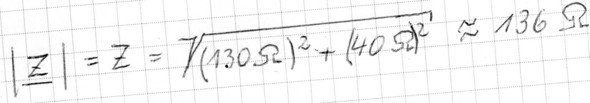
Lösungsvorschlag: (Rechnung in Teilen gekürzt dargestellt)
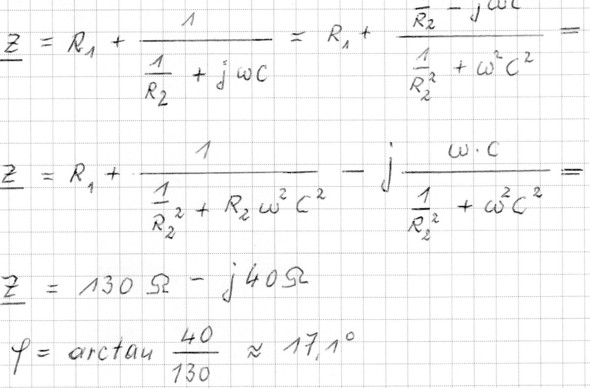
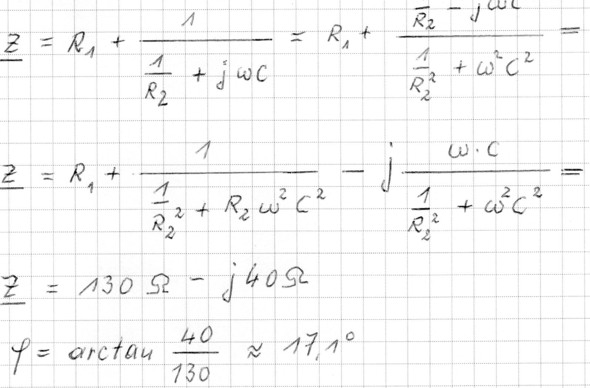
error - Der Phasenwinkel ist negativ. In diesem Fall eilt die Spannung der Stromstärke um 17,1° hinterher.
bzw warum ich 1/R2 direkt in die formel von Xc schreiben kann.
Ohne komplexe Wechselstromrechnung kann der Phasenwinkel aus dieser Aufgabe nicht berechnet werden. Komplexe Größen sind mit einem Unterstrich versehen. Das "j" ist die imaginäre Einheit ( j = sqr(-1) ). Allein mit den Beträgen kann man die Aufgabe nicht lösen. Für die Parallelschaltung von C und R2 habe ich die Leitwerte (Blindleitwert Yc und Wirkleitwerkt G) verwendet. Das sind die reziproken Werte von Blindwiderstand Xc und Wirkwiderstand R. Ansonsten kann ich nur auf das Rechnen mit komplexen Zahlen verweisen.
@Halswirbelstrom Könnte ich auch erst Xc berechnen und dann über Z=R1+(R2*Xc)/(R2+Xc)
Z berechnen. Vorausgesetzt ich habe Xc als komplexe Größe berechnet ?
Kleine Ergänzung
Scheinleitwert Y´ und Scheinwiderstand Z´ der Parallelschaltung von R2 und C
Y´=1/R2 + jωC = 0,01 S + j · 0,005 S
φi = arctan 0,005 / 0,01 ≈ 26,6° bzw. φu = - 26,6° (Phasenwinkel)
Y´= √{ (0,01 S)2 + (0,005 S)2 } = 0,01118 S → Z´= 1 / Y´= 89,44 Ω
Z´= 89,44 Ω · exp (- j · 26,6°) = 89,44 Ω · cos (-26,6°) + j · sin (-26,6°)
Z´= 80 Ω - j · 40 Ω
Stromstärke I´
I´= U´/ Z´= 5 V · exp (j · 0°) / 89,44 Ω · exp (-j · 26,6°) = 0,0559 A · exp (j · 26,6°)
φi´ = 26,6° bzw. φu´ = - 26,6° (Phasenwinkel)
Betrag der Gesamtstromstärke I
I = I´= 0,0559 A
Gesamtspannung U0
U0 = I · Z = 0,0559 A · exp (j · 0°) · 136 Ω · exp (-j · 17,1°) = 7,6 V · exp (-j · 17,1°)
Blindleistung Q
Q = Ueff · Ieff · sin φ = 7,6 V · 0,0559 A · sin 17,1° ≈ 0,125 VA
Wirkleistung
P = Ueff · Ieff · cos φ ≈ 0,41 W
Ich bin mir nicht sicher wo genau dein Problem liegt, versuche es aber mal:
Um die von der Schaltung aufgenommene Wirk- und Blindleistung zu berechnen musst du erst die Impedanz der Parallelschaltung von Kondensator (X) und Widerstand (R2) berechnen und zu R1 hinzurechnen. Über die resultierende Gesamt-Impedanz kannst du dann Phi bestimmen.
Wenn du das ganze zeichnen möchtest: der Kondensator hat nur Imaginär (y-Achse), der Widerstand nur Realanteil (x-Achse). Per parallelverschieben kommst du auch so zum Ergebnis.
Könnte ich dir da weiter helfen?
Hallo Halswirbelstrom und danke für deine Antwort. Nur kurz zur vorgehensweise: du hast die Impedanz von r2 und C ausgerechnet und mit R1 addiert? Kannst du mir noch was zum j sagen (komplexe zahlen evt ? ) da meine formel für Xc=1/omega*C lautet. Mir erschließst sich nicht woher die 1 aus dem 1/(..) stammt. bzw aus welcher formel