Kann mir wer bei der Aufgabe helfen - Satz des pythagoras?
Bei Aufgabe 6d) Ich komm da echr nicht mehr weiter

4 Antworten
Hi,
β ist der rechte Winkel, also ist b die Hyptenuse und demnach gilt:
a² + c² = b²
a = 3,4 cm = 34 mm,
demnach:
b² = 34² + 51² => b = 61,3 (gerundet)
LG,
Heni
Einheitlich Maßeinheiten verwenden. z.B. mm
3,4 cm = 34 mm
Naja Formel umstellen.
b²= c²-a²
<=> b²=5,1²-3,4²
b²= 14,45 | Wurzel
b= 3,8cm
...
Umfang= a+b+c, Umfang= 3,4+3,8+5,1 cm
Umfang= 12,3 cm
...
Flächeninhalt= (g*h)/2
Flächeninhalt= (5,1*3,4)/2
Flächeninhalt= 8,67cm²
Dass ich die Seite a mit der Seite b vertauscht habe, ja.
Hallo,
ich versuche es einmal. Die Seite c = 51mm, die Seite a = 34mm und Winkel beta=90°.
Weil der Winkel beta = 90° ist, handelt es sich um ein rechtwinkliges Dreieck. Jetzt ergibt sich ein Problem aus der Aufgabenstellung. Wenn der Winkel beta=90° ist, dann sind die Winkel alpha u. gamma auf jeden Fall kleiner als 90°. Die Seite die gegenüber von beta liegt, wird üblicherweise als die Seite b bezeichnet. Das ist hier aber nicht möglich, weil beta=90° und damit ist die gegenüber liegende Seite, die längste Seite im Dreieck und damit die Hypotenuse und die wird üblicherweise als die Seite c bezeichnet. Das bedeutet, wenn man nun den Satz von Pythagoras anwendet und nach Seite b umstellt, die Werte einsetzt und ausrechnet, bekommt man ein falsches Ergebnis. Beispiel:
c² = a² + b² / - a²
c² - a² = b² / Jetzt Werte einsetzen
51² - 34² = 2601 - 1156 = 1445
1445 = b² / Jetzt Wurzel aus b²
= 38,013 =b (Auf drei Stellen genau.)
Ein rechtwinkliges Dreieck mit a=34mm, b=38mm, c=51mm mit beta = 90° ist unmöglich (Siehe Skizze unten).
U.U. ein Fehler in der Aufgabenstellung.
Wenn man das rechtwinklige Dreieck mit den Werten a=34mm, c=51mm und beta =90° via SIN-/COS-Satz berechnet ergeben sich folgende Werte für das rechtwinklige Dreieck (Berechnungsform:Seite,Seite,Winkel (SSW))
a=34mm, b=61.29mm, c=51mm, alpha=33.69°, beta=90°, gamma=56.31°
Damit zeigt sich, dass die Seite b die Hypotenuse ist und damit eigentlich die Seite c.
Aus diesen Daten ergibt sich der Umfang U=a+b+c = 34+61.29+51 = 146.29mm
Aus diesen Daten ergibt sich die Fläche A=(a*c)/2 = (34*51)/2 = 867mm²
Ich hoffe es hilft. Gruesse e1

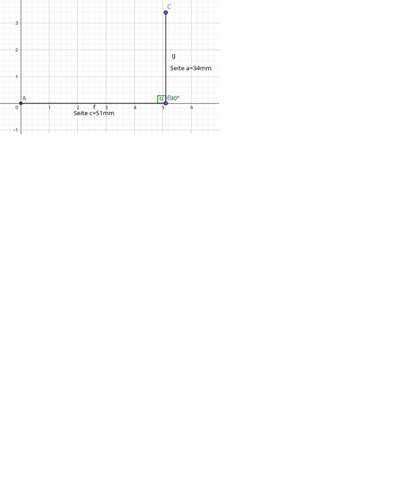
In diesen Ansatz zur Lösung der Aufgabe hat sich ein Fehler eingeschlichen.