kann mir jemand bei einer Matheaufgabe zu quadratischen Gleichungen helfen?
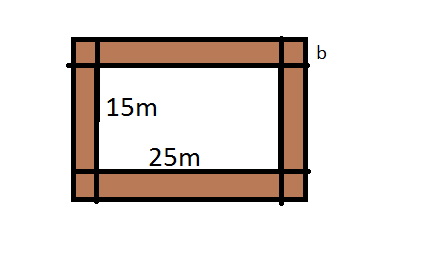
Ein rechteckiger Garten ist 25 Meter lang und 15 Meter breit. Um ihn herum führt ein weg von gleichbleibender Breite. Der weg beansprucht eine fläche von 84 m². Wie breit ist der Weg?
5 Antworten
B sei die breite
84 = 2×15×b + 2x25xb + 4b^2
84 = 4b^2 + 80b
b^2 + 20b - 21 = 0
Mit pq Formel und aus dem Sachzusammenhang folgt b=1m
Ich hab mal ne wunderschöne Skizze erstellt xD
Die Breite des Weges nennen wir der Einfachheit halber b. Wie du siehst lässt sich der Weg in 8 Teile einteilen:
2 Rechtecke an den langen Seiten (25m * b)
2 Rechtecke an den kurzen Seiten (15m * b)
4 Quadrate an den Ecken (b * b)
Addieren wir diese Flächen zusammen ergibt dass:
A= 2 * 25m * b + 2 * 15m * b + 4 * b * b = 80m * b + 4 * b²
Laut Aufgabe gilt A = 84 m². Also
84 m² = 80m * b + 4* b² | - 84 m²
0 = 4 * b² + 80m * b - 84 m² | /4
0 = b² + 20m * b - 21 m² | pq-Formel
b= -20m/2 ± sqrt((20m/2)²-(-21m²))
b= -10m ± sqrt(100m² + 21m²)
b= -10m ± sqrt(121m²) = -10m ± 11m
Der Weg ist also entweder 1 Meter oder -21 Meter breit. Da eine negative Breite keinen Sinn macht wird er einen Meter breit sein.
LG Simoris
PS: Wenn man will kann man das natürlich auch mit abc- bzw. Mitternachtsformel machen und spart sich dann das durch vier teilen.
sqrt() steht für ne Wurzel.
Hallo PatayaGF,
Franks Antwort würde stimmen, wenn man den Umfang des Gartens in eine Linie legen würde und dann darüber ein Rechteck bilden würde. So fehlen aber die vier Ecken, d.h. wir hätten vier Stücke Wegs, die an den Ecken nicht miteinander verbunden sind. Um diese Ecken zu berücksichtigen müssen wir zu der Rechnung 4x² hinzufügen. Also:
2 * L * x + 2 * B * x + 4 x² = 84 m²
Kannst Du das selbst lösen?
Gruß Friedemann
Wieder mal eine Sache der Übersetzung.
http://dieter-online.de.tl/Deutsch_Mathematisch.htm
Das innere Rechteck ist 25 * 15 = 375 m² groß.
Das äußere Rechteck hat noch einen gleichmäßigen Rand von x m,
also links x Meter und rechts x Meter.
Daraus folgt für das äußere Rechteck
(25 + 2x) * (15 + 2x) = 375 + 84 weil ja die Umrandung 84 m² ausmacht
375 + 50x + 30x + 4x² = 459 | ordnen
4x² + 80x + 375 = 459 | -459
4x² + 80x - 84 = 0 | /4
x² + 20x - 21 = 0 | p,q-Formel p = 20 q = -21
x₁,₂ = -10 ± √(100 + 21)
x₁,₂ = -10 ± 11 uns interessiert nur die positive Lösung
x = 1
Damit kennen wir die Breite des Wegs: 1 m
2x 25m + 2x 15 = Umfang des Rechteck (80m)
Fläche (84m2) : 80 = 1,05m
Kann das stimmen?