K-Vektorräume und K^n?
Hallo!
Hier ein Diagramm:
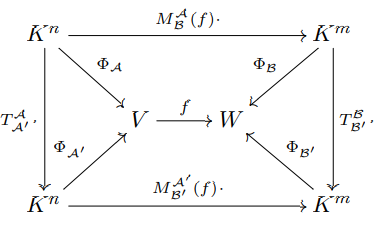
[(K ist Körper; V,W sind K-Vektorräume; M(f) ist Darstellungsmatrix bzgl. angegebener Basen; T sind Basistransformationsmatrizen und f ist K-Lineare Abbildung)]
Also eigentlich verstehe ich alles ganz gut rund um dieses Thema. Dennoch geht es um diese Phi´s in dem Bild...
Die Abbildungen Phi sind Isomorphismen. Diese Isomorphismen existieren hier, da vorher bedingt wurde, dass V eine Basis A=(a_1,...,a_n) und W die Basis B=(b_1,...,b_m) hat und somit V isomorph zu K^n und W isomorph zu K^m ist.
Naja meine Frage ist: Ist es nicht überflüssig über die K^n und K^m zu gehen? Ich meine könnt ihr mir ein Beispiel eines endlich dimensionalen K-Vektorraums geben, welcher nicht direkt der "Form" K^d entspricht? Ich meine so Funktion- und Folgenräume sind doch alle nicht endlich dimensional... Bedeutet es gibt doch gar keinen endlich dimensionalen K-Vektorraum, welcher NICHT einfach nur K^n ist. Wieso brauche ich dann in diesen Diagrammen diese Isomorphismen? Wieso wird V als K^n übersetzt, obwohl V=K^n?
Oder habt ihr ein Beispiel ?
Danke und LG Max!
2 Antworten
Hallo, ich bin momentan nicht ganz in dem Thema drin, aber meiner Überlegung nach müsste der Vektorraum aller K-Wertigen nxm-Matrizen (schreibt man oft als K^(nxm)) ein Beispiel für dich sein: ist nicht direkt K^(n*m), aber isomorph dazu.
Falls su noch ein abstakteres Beispiel suchst, dann wirst du beim Dualraum eines endlichdimensionalen Vektorraums fündig.
Betrachte mal den Vektorraum aller Polynome über R mit Grad kleiner gleich n. Dieser ist n+1 dimensional und entspricht nicht der Form K^(n+1).
Uh ja gutes Beispiel. Da hätte ich drauf kommen müssen.... danke !
Stimmt! Auch ein gutes Beispiel Danke! Der Matrizenraum ist auch noch Isomorph zu L(V,W). Die Menge aller Linearen Abbildungen zwischen den K-Vektorräumen V und W, wobei n die Dimension von V und m die Dimension von W ist. Also noch ein weiteres Beispiel. Danke :D