Ist Eine Asymptote eine Gerade oder eine Kurve, die sich einem Graph einer Funktion immer mehr annähert ohne sie zu schneiden?

Schau Dir den Verlauf von f(x) = sin(x) / x an. Der Graph nähert sich der Asymptote an, schneidet diese aber auch.

Antwort

Eine Asymptote kann eine Kruve sein, aber auch eine Gerade, weswegen man Sie in der Mathematik als "Line" (Line: Gerade oder Kurve) bezeichnet. Das heißt aber nicht, dass eine Asymptote die Funktion nicht schneiden kann (z.B. bei f(x) = sin(x) mit der Asymptote an x = 0).

Weiteres

Das geht aus der allgemeinen Definition einer Asymptote hervor: Eine Asymptote ist in der Mathematik eine Linie (Kurve, häufig als Gerade), der sich der Graph einer Funktion im Unendlichen immer weiter annähert. Eine „Sonderform“ ist der asymptotische Punkt, bei dem die Annäherung nicht im Unendlichen stattfindet. (Definition geklaut von Winkipedia)

Eine Asymptote, welche eine Gerade ist, bezeichnet man als Gerade Asymptote. Eine Asymptote, welche eine Kurve ist, bezeichnet man als Nichtgerade Asymptote. Ein asymptotische Punkt wird verallgemeinert als Häufungspunkt einer Kurve gesehen, wemnach kann auch eine Hebbare Definitionslücke ein asymptotischer Punkt sein.

Gerade Asymptote

(f(x) := Kurvengleichung | A(x) := Gerade Asymptotengleichung)

Nichtgerade Asymptote

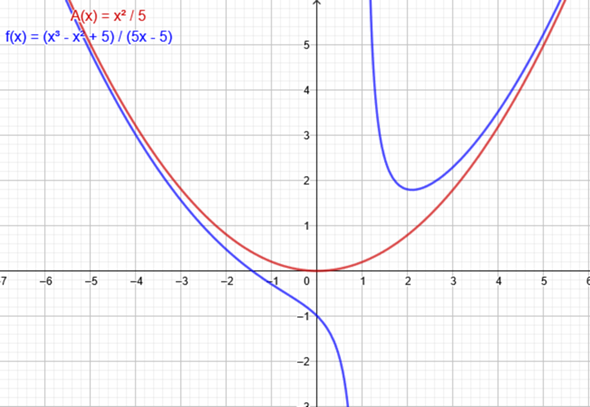
(f(x) := Kurvengleichung | A(x) := Nichtgerade Asymptotengleichung)

Asymptotische Punkt

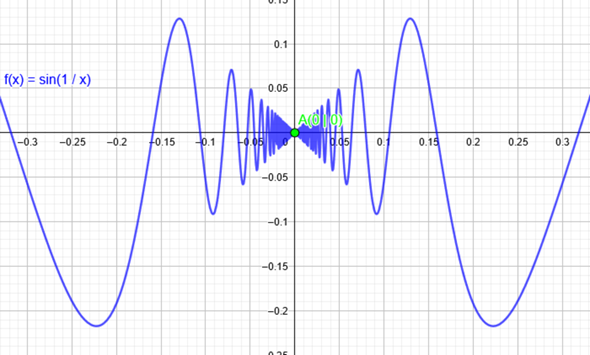
(f(x) := Kurvengleichung | A := Asymptotische Punkt)

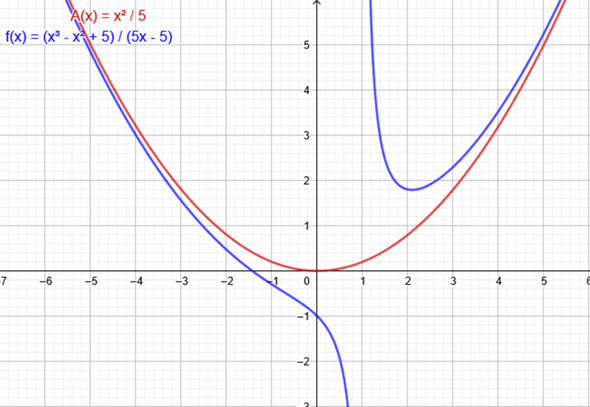
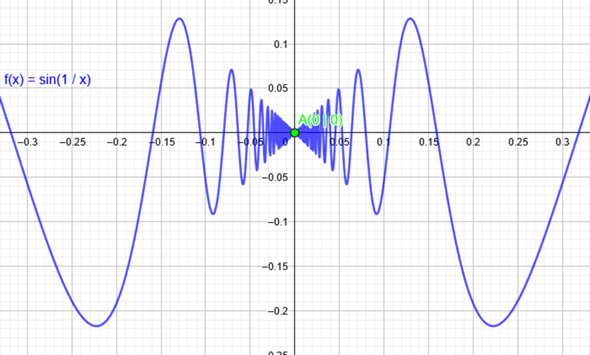
Beides

e^(-x) + x² Mal in Geogebra eingeben

Eine Asymptote ist eine Gerade. Und es ist umgekehrt. Eine Kurve nähert sich einer Asymptoten ohne sie zu schneiden.

Eine Assymptote kann auch die Gerade der funktion schneiden, schau mal die assymptote von Sinus im Punkt x=0 an