Ist die Zahl 0 ne gerade oder ungerade Zahl?
frage steht oben :D ich hab heute gefühlte tausend Leute gefragt und jeder hat was anderes gesagt...
10 Antworten
Statt vieler Worte sollte eine mathematische Frage auch mathematisch exakt beantwortet werden, wann ein Argument gerade ist:
Die Funktion lautet: f(x) = ((x mod 2) == 0)
f( 0 ) = true (wahr) , denn 0 Modulo 2 ist 0
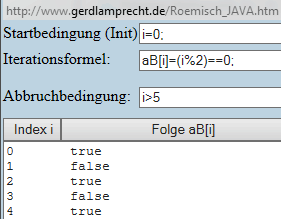
Schon die unmittelbare Abschauung zeigt, dass 0 zu den geraden Zahlen zählt. Jede zweite ganze Zahl ist gerade. Da braucht man nur z.B. von 4 aus abwärts zu zählen, dann kommt man auf 2 und 0, weiter auf -2 usw.
Das ist natürlich kein Beweis, ist aber nützlich für die Vorstellung von Zahlen.
Auf der DVD von Professor Beutelspacher erwähnt dieser, dass die Null gerade sei! Irgendwie ist es ja auch logisch: Die Formel für eine gerade Zahl ist doch 2 * n. Setzt du für n beispielsweise 1 ein, so bekommst du 2 heraus. Die nächste gerade Zahl liegt 2 weiter, bei 4 usw. Gehst du immer 2 Zahlen rückwärts, so kommst du bei 2 - 2 zu Null, dann zu -2 usw. Das ist doch in sich konsistent!
Insbesondere ergibt sich 0 als gerade, wenn Du in der genannten Formel 2 * n das n = 0 setzt. Dafür braucht man noch nicht einmal von irgendwo rückwärts zu zählen ;)
@appletman:
Kanst du Gedanken lesen? Du hast deine Antwort zur selben Zeit abgeschickt wie ich.
Wenn es nicht sowie etliche (schon erwähnte) Gründe gäbe, aus denen 0 logischerweise als gerade anzusehen ist, so müsste 0 zumindest per Defintion gerade sein, damit zahlreiche Gesetze der Zahlentheorie allgemeingültig sind.
Eine ganze Zahl ist gerade, falls sie ein ganzzahliges Vielfaches von 2 ist. Insbesondere ist
0 = 0 * 2 ein Vielfaches von 2, also ist 0 gerade.