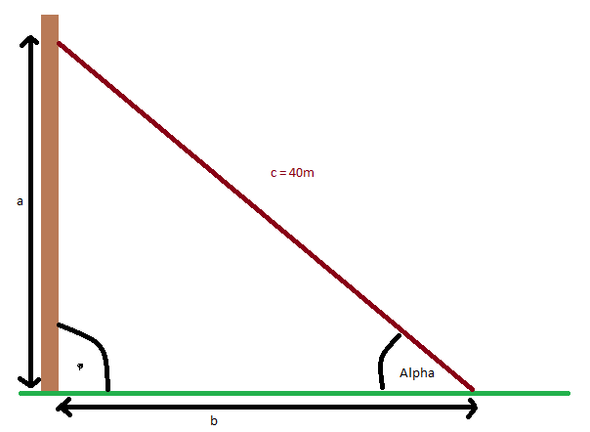
Wie löst man diese Textaufgabe?
Hallo, wir haben gerade das Thema Trigonometrie und ich wollte fragen, wie man diese Aufgabe löst. Und zwar: Ein Sendemast soll mit vier Seilen von je 40m Länge gehalten werden. Der Neigungswinkel Alpha der Seile soll jeweils 55° groß sein. In welcher Höhe müssen die Seile befestigt werden? Wie weit vom unteren Ende des Mastes müssen die Seile befestigt werden? Könnt ihr mir dazu vielleicht auch ein paar Rechnungen aufstellen und mir logisch erklären?
2 Antworten
Die benötigst den Sinus und den Cosinus um diese Aufgabe zu lösen. Du hast ein Dreieck und weißt, dass die Hypothenuse 40 Meter lang ist. Die Gegenkathete ist die Höhe in der das Seil befestigt wird:
Sin(55°)*40m=32,766 Meter
Die Ankathete ist die Distanz der Befestigung zum Mast.
Cos(55°)*40m=22,943 Meter
Um das besser zu verstehen solltest du dir eine Zeichung machen und dir die Definition von Sinus und Cosinus im Internet durchlesen.
https://de.serlo.org/mathe/terme-gleichungen/gleichungen/trigonometrische-gleichungen/sinus-kosinus-tangens
Du hast alpha = 55° und c = 40m gegeben.
Du suchst die Höhe = a und den Abstand zum Ende des Mastes = b.
Einfach in die trigonometrischen Gleichungen einsetzen und nach a und b auflösen.