Ich habe ein mathematisches Problem, ich weiß aber nicht, wie ich es lösen soll, vielleicht kann mir jemand helfen?
Hallo,
ich bin absolut kein Mathegenie.
Dennoch beschäftige ich mich manchmal mit kleineren mathematischen Aufgaben...
Ich habe mir überlegt, wie viele Möglichkeiten es gibt, die Ziffern 2200 in beliebiger Reihenfolge anzuordnen...
Ich kam durch Ausprobieren aller Möglichkeiten auf 6 verschiedene Konstellationen! 2002, 2020, 2200, 0220, 0202, 0220!
So weit so gut! Jedoch wollte ich eine Formel finden, mit der ich die Gesamtanzahl dieser Möglichkeiten auch berechnen kann...
Ich dachte zuerst an das Binärsystem... Aber das hat mir leider auch nicht weitergeholfen...
Hat jemand von Euch eine Idee?
Ich weiß, es ist für echte Mathematiker eine lächerlich einfache Aufgabe... Aber ich komme leider nicht drauf. Vielleicht kann mir jemand von Euch weiterhelfen! :)
Liebe Grüße,
Kai
4 Antworten
Das lässt sich auch schön verallgemeinern.
Nimm an du hast m unterschiedliche Zahlen, und die Zahlenfolge soll insgesamt die Länge n haben.
Außerdem soll jede der m Zahlen genau
mal vorkommen, dann gilt für die Gesamtzahl der möglichen Zahlenfolgen mit diesen Eigenschaften:
wobei
Beispiel:
Angenommen du hast die 3 gegebenen Zahlen 0, 1, 2 und die 0 soll 2 mal vorkommen, die 1 soll 5 mal vorkommen und die 2 soll 8 mal vorkommen.
Damit suchst du also Zahlenfolgen von der Form (hier ein Beispiel):
011101212222222
Die Zahlenfolge ist also von der Länge n = 15 mit m = 3
und z_1 = 2, z_2 = 5, z_3 = 8
Die Anzahl der möglichen Folgen wäre damit:
Dazu müsstest du definieren, ob du immer je zweimal die gleiche Zahl hast oder ob das auch mal 3 oder 4 verschiedene sind.
Ich hätte an die geringstmögliche Anzahl an verschiedene Zahlen gedacht...
Du musst nur zählen wie viele Möglichkeiten es gibt die zwei Zweien auf die vier Plätze aufzuteilen.
Also ziehen wir für jede Zwei eine von vier Platznummern, ohne Zurücklegen. Die Anzahl der Möglichkeiten beträgt:
Das ist der sogennante Binomialkoeffizient. Im Wikipedia-Artikel steht auch wie er sich kombinatorisch begründen lässt.
Du hast 0022 vergessen
https://www.studienkreis.de/mathematik/permutation-variation-kombination/

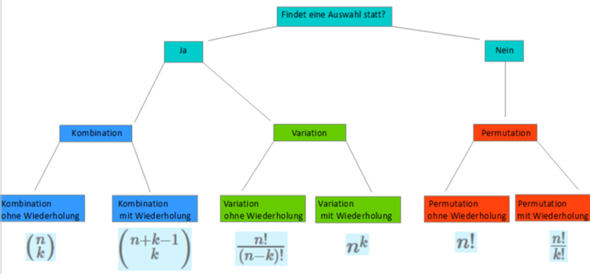
ich denke das war ein Tippfehler. du hast das echt Klasse erklärt
... und 0220 dafür doppelt aufgelistet.