Grenzkosten nicht linearer Kostenfunktionen?
Die Grenzkosten entsprechen den Kosten, die durch die Produktion einer zusätzlichen Mengeneinheit eines Produktes oder einer Dienstleistung entstehen und sind als die erste Ableitung der Kostenfunktion definiert. Bei linearen Funktionen entspricht die Steigung den zusätzlichen Kosten. Müsste bei nicht linearen Funktionen h=1 sein und nicht gegen Null laufen?
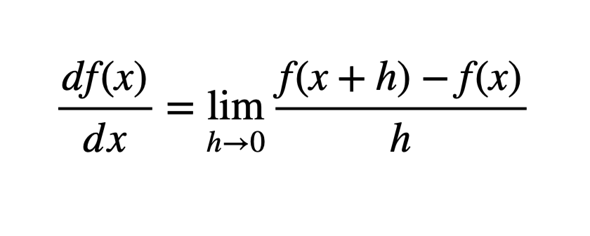
3 Antworten
Was du gepostet hast ist der Ansatz , um die Ableitung einer f(x) zu bestimmen . Das gilt für alle Fkt . Und es geht immer h gegen Null.
Wenn die Grenzkosten entsprechen der ersten Ableitung der Kostenfunktion, dann ist bei einer KFkt mit Grad 3 die Ableitung eine Fkt mit Grad 2 . Auch bei nichtlinearen Fkt sind das die zusätzlichen Kosten .
Lineare Funktion sind ja auch differenzierbar. Natürlich kannst du einfach ein Steigungsdreieck an deine Funktion anlegen, wenn sie linear ist (d.h. für h=1 einsetzten) und da sollte aber das selbe rauskommen, als wenn du den Grenzwert bestimmst.
h müsste 1 sein? Warum? Das ist nicht mehr die Steigung zwischen zwei infinitesimal nahe beianderliegenden Punkten, so wie es im Bild steht stimmt es.
f(x)=Kostenfunktion, f’(x)=Grenzkosten
Naja das ist ja offensichtlich.
Die Kostenfunktion gibt halt die Kosten an für x Einheiten + Grundkosten, die Grenzkosten für eine Einheit. Ist halt die Steigung davon. lol
Reicht das schon?
Überleg es dir doch so
Kostenfunktion(x) = mx + b
So, m sind die Kosten für eine Einheit, b die ,,Grundkosten", die Ableitung davon ist nur noch m, also.
Im linearen Fall macht es Sinn so zu argumentieren
Danke für deine Antwort. Meine Frage bezieht sich aber auf nicht lineare Funktionen
h müsste 1 sein laut der Definition der Grenzkosten. Dann ist es eine Sekante, aber die Grenzkosten sind als die erste Ableitung definiert. Ich verstehe nicht warum die Grenzkosten der ersten Ableitung der Kostenfunktion entsprechen.