Für welche Winkel gilt cos α=-0,5?
Lösung: cos α = -0,5 für a₁ = 120°; α₂= 240°
Frage: Wie kommt man darauf?
Wenn man sich das im Einheitskreis vorstellt, dann weiß ich, dass auf der x-Achse (wegen cos) -0,5 genau in der Mitte von 0 und -1 liegen muss. Aber den Winkel davon kann man sich ja schlecht vorstellen.
Oder gibt man den ersten Winkel (a₁ = 120°) in den Taschenrechner ein und den zweiten Winkel ermittelt man durch Überlegung am Einheitskreis?
4 Antworten
Kannst du mir vielleicht ein Bild vom Einheitskreis schicken, wo cos (120) = -cos (60). Beide müssen ja bei bei cos -0,5 sein. Wie geht das aber bei - cos (60) (bei mir wären cos 0,5).
?
Natürlich kann ich das machen.^^:
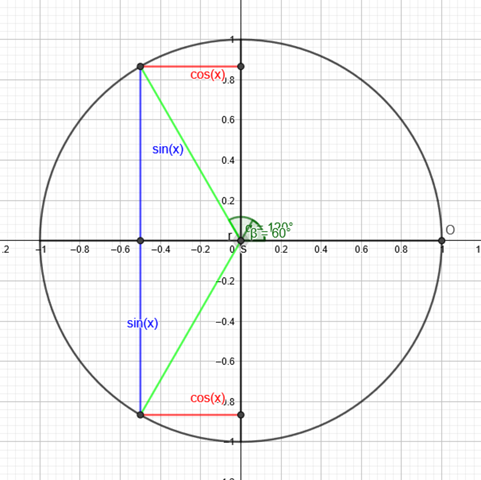
Warum ist der kosinus nicht rechts eingezeichnet?
cos(60) geht zwar 0,5 nach rechts, aber durch das minus verläuft es nach links.
SInus bleibt dabei gleich.
(-cos(60)=-1/2=-0,5)
Man kann das auch rechnereich betimmen, jedoch werden Sie das niemals im Leben bruchen, außer Sie wollen Mathematik studieren...
Visuell lässt es sich aber besser an der Funktion cos veranschaulichen:
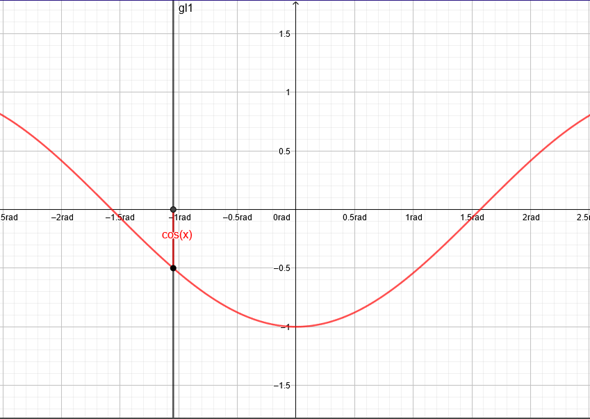
(f(x)=-cos(x) und s(x)=-PI/3 rad)
(-PI/3 rad=-60°)
Ich hoffe, dass ich weiterhelfen konnte.^^
Bei weiteren Fragen stehe ich Ihnen natürlich zur Verfügung. uwu
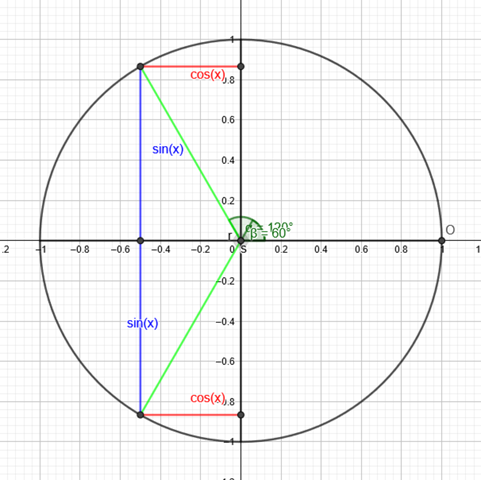
Vielen Dank! Aber cos (60) muss ohne jetzt dem Vorzeichen doch im ersten Quadranten liegen? Und nicht im dritten Quadranten, also müssten sich ja die Dreiecke ja überschneiden bzw. gleich sein von beiden Cosinuswerten (wenn man cos (60) dann mit -1 multipliziert —> 2. Quadrant)! Und eigentlich doch nicht wie in ihrem Bild, irgendwie ist mir das unklar?
bitte um eine Antwort 🥺
denn Ihres wäre doch cos 240 Grad, aber wir brauchen doch cos (60), den wir später mit -1 multiplizieren und der dann auf die negative x-Achse wandert? Oder, wenn ich mich nicht täusche. 😫
Aber cos (60) muss ohne jetzt dem Vorzeichen doch im ersten Quadranten liegen?
Bei den Eiheitskreis wäre das korrekt.
Mit den Minus ist es dann im zweiten Quadranten.
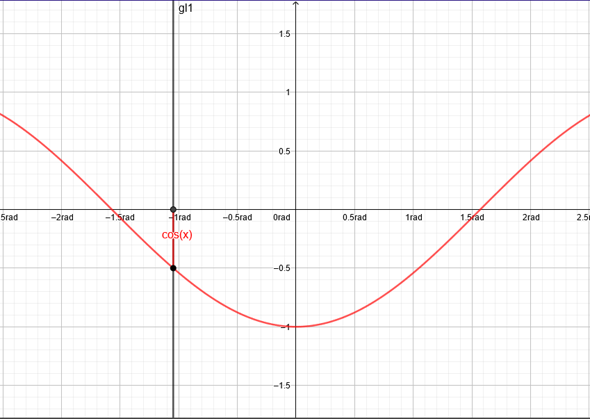
In der Funktion cos(x) wäre es auch im ersten Quadranten, jedoch liegt es wegen den Minus (-cos(x)) im vierten Quadranten.
Und nicht im dritten Quadranten, also müssten sich ja die Dreiecke ja überschneiden bzw. gleich sein von beiden Cosinuswerten (wenn man cos (60) dann mit -1 multipliziert —> 2. Quadrant)!
So ist es.
Ich denke, dass ich es wohl unübersichtlich dargetellt habe...
Beide Werte gehöhren zum oberen linken Punkt.
Den linken unteren Punkt habe ich nur zu Veranschaulichung plaziert, um z.B. die Frage vorzubäugen, was paaiert wenn vor den sin(x) ein Minus steht.
Und eigentlich doch nicht wie in ihrem Bild, irgendwie ist mir das unklar?
Es ist doch wie in meinem Bild?
Beide Werte sind oben links.
Das unten links war nur für den Fall von -sin...
denn Ihres wäre doch cos 240 Grad, aber wir brauchen doch cos (60), den wir später mit -1 multiplizieren und der dann auf die negative x-Achse wandert? Oder, wenn ich mich nicht täusche. 😫
Nein, nein.
Sie täusen sich nicht.
Unten links wäre unter anderen cos(240°) oder auch -cos(-60°)=-0,5=-cos(60°) und -sin(60°)=-0.866025403784...
(Zur Erklährung siehe meine Vorhärige Antwort.)
Am Einheitskreis: du zeichnest die -0,5 wie von dir beschrieben ein und gehst von diesem Punkt senkrecht nach oben und unten. Die beiden Schnittpunkte mit dem Kreis verbindest du mit dem Mittelpunkt des Kreises und hast deine beiden Winkel.
Am Taschenrechner: du brauchst die Umkehrfunktion des Cosinus, den Arcuscosinuns. Am Taschenrechner oft als "cos-¹" zu finden.
Wenn man sich das im Einheitskreis vorstellt, dann weiß ich, dass auf der x-Achse (wegen cos) -0,5 genau in der Mitte von 0 und -1 liegen muss. Aber den Winkel davon kann man sich ja schlecht vorstellen.
Geh von x = -0,5 senkrecht nach oben. Der Schnittpunkt mit dem Kreis, die Punkte (0|0) und (-1|0) bilden ein gleichseitiges Dreieck, also Innenwinkel 60°. 180° - 60° ist also der Winkel, um den sich der Zeiger gedreht hat.
Man kann auf verschide Wege darauf kommen.Z.B. Rechnerich und Zeichnerich.Ich erkläre gerne beides:
PS.
Es gibt unendlich viele Ergebnisse für "cos(x)=-0,5", jedoch wird das leider fast nie gesagt bzw. erklärt...
Zeichnerich:
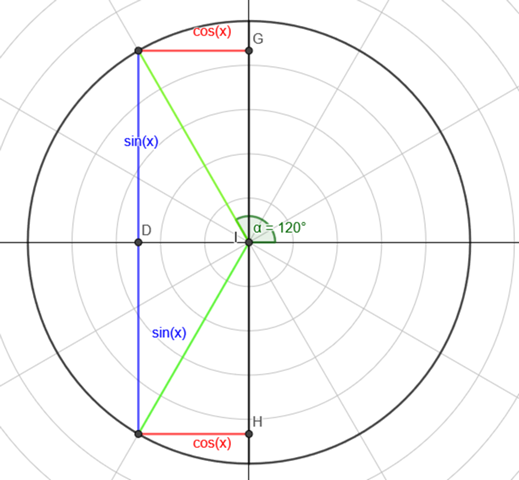
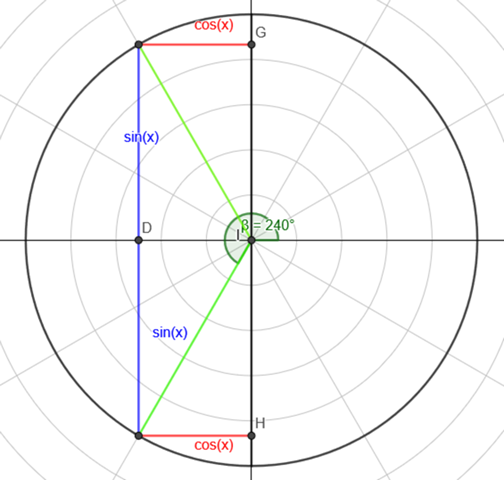
Der Einheitskreis...
Zeichnet man cos(x)=-0.5 ein so kann man die möglichen Winkel ablesen.Hier ist der rote Strich -0,5, da er -0,5x geht.
Rechnerich:
cos(x)=-0,5 | arccos (man kann auch wenn man kein Leben hat die Eigentliche Kosinusfunktion umstellen, aber das ist mir hier zu viel arbeit)
arccos(cos(x))=arccos(-0,5)
x=arccos(-0,5)={..., -600°, -480°, -240°, -120°, 120°, 240°, 480°, 600°, ...}
Da könnt man sich fragen, wieso kommen teilweise Ergebnisse mit über 360° und gar negative Gradzahlen raus?
Simpel! Man kann diese Ergebnisse Mittels Kosinusfunktion ermitteln. Hierbei wird in allgemeinen die gleichung ((e^(xi)+e^(-xi))/2) bzw. die dazugehörige Taylorreihe genutzt. In diessen kann man auch negative Werte, wie auch viel grrößere eigeben und sie kalkulieren.
Z.B. Ergibt cos(-1235721720) auch -0,5.
Leider kommt sowas erst viel zu spät in der Bildung ran, weswegen sich leider viele die Falschinformation merken, dass nur Werte zwischen 0° und 360° bei cos(x)=a (0<a<1) rauskommen können. Es kommen dabei immer unendlich viele Ergebnisse raus - selbst bei komplexen Zahlen.
Ich hoffe, dass ich weiterhelfen konnte.^^
Bei weiteren Fragen stehe ich Ihnen natürlich zur Verfügung. uwu
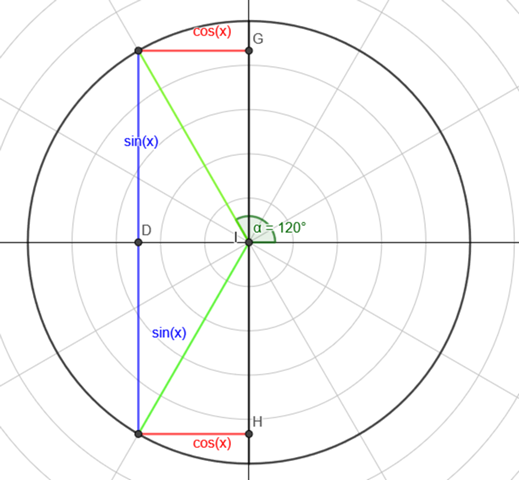
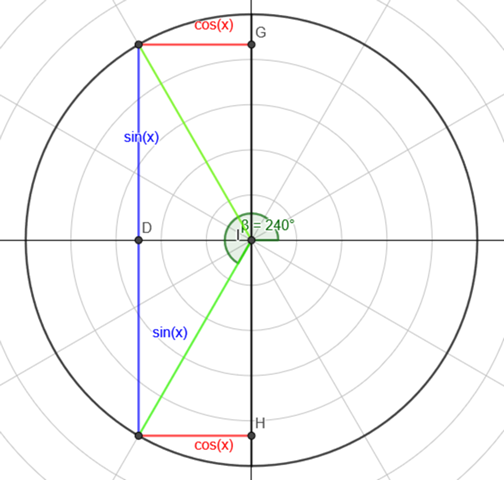
Kannst du mir vielleicht ein Bild vom Einheitskreis schicken, wo cos (120) = -cos (60). Beide müssen ja bei bei cos -0,5 sein. Wie geht das aber bei - cos (60) (bei mir wären cos 0,5).
?
PS.
cos(60°)=0,5
jedoch gilt
-cos(60°)
und das ist
-0,5
(-cos(60°)=-0,5)