Frage zur Längenkontraktion (SRT)?
Hi,
habe mal eine Frage zu folgender Aufgabe:
In einem Linearbeschleuniger wird ein Elektron auf die Geschwindigkeit v=0,6c beschleunigt. Anschließend durchfliegt es mit konstanter Geschwindigkeit eine Strecke der Länge s=9m.
Wie lange braucht das Elektron, um die Strecke zu durchfliegen?
(Lsg.: t=50ns)
Nunja.... Müsste es nicht eigentlich so sein, dass die Strecke innerhalb des Ruhesystems gleich bleibt und nur von der Erde aus die Strecke kürzer erschient, oder liege ich jetzt komplett falsch? :o
VG
2 Antworten
Hallo 007arielle,
die Aufgabenstellung ist eine Falle. Bei Geschwindigkeiten dieser Größenordnung (0,6c) schaltet wohl fast Jeder sofort erst mal auf „kompliziert“, dabei ist die Sache ganz einfach, wie @michiwien schon geschrieben hat:
Mit Δt ist t gemeint, und mit Δx=s. Es handelt sich ja um Koordinatendifferenzen im Laborsystem Σ, in dem sich das Elektron und nicht die Strecke bewegt. Es war nicht von einer mit dem Elektron mitbewegten Uhr die Rede.
Müsste es nicht eigentlich so sein, dass die Strecke innerhalb des Ruhesystems gleich bleibt…
Obacht! Es gibt nicht „das Ruhesystem“, sondern z.B. das Ruhesystem Σ' des Elektrons; es ist das Koordinatensystem, in dem das Elektron nach der Beschleunigung ruht. In Σ' ist der Erdboden gewissermaßen ein riesiges, mit (-0,6c;0;0) bewegtes Laufband, das die Strecke mit sich zieht, auch den Linearbeschleuniger, der das Elektron auf 0 abbremst, bevor sich die Strecke an ihm vorbei bewegt.
Oft hört man, das Elektron müsse „aus der eigenen Sicht“ (also in Σ') nur eine Strecke
durchfliegen, in diesem Falle also „nur“ 0,8s=24ns·c. Aber das ist falsch gedacht, denn Σ' ist ja das Ruhesystem des Elektrons, also Δx'=0. In Σ' bewegt sich die Strecke und ist um diesen Faktor 1/γ kürzer gemessen.
Das Wort „Längenkontraktion“ ist dabei eigentlich ein alter Zopf, an dem selbst Verfechter der Relativitätstheorie (es gibt auch Gegner, die sie jedoch meist nicht verstanden haben) festhalten, ebenso wie an „Zeitdilatation“.
Es ist immer möglich und m.E. auch sinnvoll (nicht erst durch die SRT), Raum und Zeit zur Raumzeit zusammenzufassen. Bei einer Verabredung brauchst Du ja auch Ort und Zeit des vereinbarten Treffens. Dieses ist ein Beispiel für ein Ereignis.
EINSTEINs ehemaliger Matheprofessor MINKOWSKI fand heraus, das in der Raumzeit ein Abstandsquadrat zwischen zwei Ereignissen definiert ist, der in Σ und Σ' identisch ist, wie das räumliche Abstandsquadrat
(3) Δs² = Δx² + Δy² + Δz² ≡ Δx°² + Δy°² + Δz°²
zweier Punkte im Raum sich durch eine Drehung Σ→Σ° nicht ändert. Es lautet
(4.1) Δτ² = Δt² – c⁻²Δs² ≡ Δt'² – c⁻²Δs'²
bzw.
(4.2) Δς² = Δs² – c²Δt² ≡ Δs'² – c²Δt'²,
von denen eines immer negativ ist, wenn nicht beide 0 sind (die Lichtgsschwindigkeit hat in Σ und Σ' gleichermaßen den Betrag c).
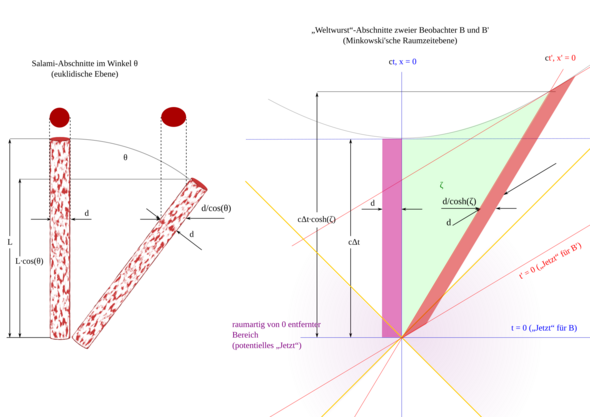
Die Spur eines Körpers in der Raumzeit wird als seine Weltlinie bezeichnet. Genauer ist es die Spur z.B. seines Schwerpunktes. Die Ausdehnung des Körper selbst könnte man besser berücksichtigen, wenn man von einem „Weltstrang“ oder einer „Weltwurst“ spräche, was leider unüblich ist. Aber ebenso wie eine Salami weder kürzer noch breiter wird, wenn man sie dreht, ist ein Zeitabschnitt auf einer relativ zu Σ bewegten Uhr U' nicht per se, sondern nur entlang der Zeitrichtung von Σ länger, und ein bewegter Körper ist nicht per se, sonder nur „quer“ zu dieser Zeitrichtung kürzer.
Die „Längenkontraktion“ ist eigentlich ein „Schrägschnitt durch die Weltwurst“; gemessen wird dabei eine Strecke Δς, die ohnehin kürzer ist als s.
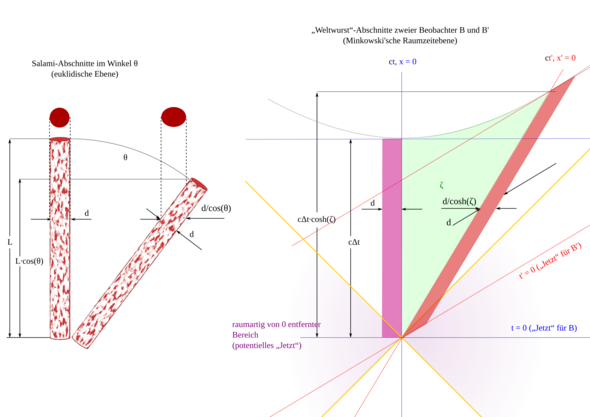
…und nur von der Erde aus die Strecke kürzer erscheint,…
Wenn schon, dann vom Elektron aus. Dabei ist „erscheint“ aber irreführend. Die Strecke sähe „aus Sicht des Elektrons“ nicht kürzer aus, sie würde als kürzer gemessen. Eine vor mir liegende Strecke oder ein mir entgegenkommender Körper sähe aufgrund eines Retardierungseffekts (ich sehe den Körper ja mit abnehmender Verzögerung, die zudem am entfernteren Ende größer ist als am Näheren) sogar langgestreckt.
Wir beobachten vom Laborsystem. Da hat das Elektron eine Geschwindigkeit von
v =0.6c = 1.8*10^8 m/s.
Die Länge im Laborsystem ist 9m.
Gesucht ist die Zeit im Laborsystem, also
t=s/v = ...=50ns
Im Ruhesystem des Elektrons ist diese zeit anders; aber das ist ja nicht gefragt ;-)
Die Aufgabe ist unvollständig formuliert, weil nur von "der Zeit" die Rede ist, als gäbe es "die" Zeit überhaupt.