Fibonacci, Tribonacci, "n-bonacci" Konstanten bestimmen?
Moin Leute, ich habe spaßeshalber (und zur Übung) die Fibonacci, Tribonacci (Zahl an Stelle n ist die Summe der drei Vorgänger) und die "Quadribnacci" (Zahl an Stelle n ist die Summe der vier Vorgänger) Sequenzen programmiert, folgendes ist mir dabei aufgefallen: die Konstanten dieser Folgen, also der Wert von
(n ist die Zahl an Stelle a der Sequenz, bei Fibonacci wäre n_5 zb. 5)
wenn a gegen ∞ geht sind die Lösungen folgender Gleichungen:
(Sagen wir mal, n sei die Anzahl an Vorgänger die wir zusammenzählen, n = 2 wäre also die bekannte Fibonacci Folge)
(Hierbei wäre die Zahl Phi, also ca. 1.618033988749895)
(Hier wäre die Zahl ca. 1.8392867552141612)
(Hier wäre die Zahl ca. 1.9275619754829254)
Allgemein gilt also: Die Konstante einer n-Bonacci Folge ist die Lösung folgender Gleichung:
Jetzt ist meine Frage, ob man diese Gleichung irgendwie "schöner" schreiben kann, also ob es irgendeine Möglichkeit gibt, diese Konstanten schnell und einfach bestimmen zu können
5 Antworten
Ja, dafür gibt es eine Iterationsformel :
Wenn du nicht weißt was eine Iteration ist, dann schaue bitte im Internet nach, auch auf Youtube.
r = (r - r ^ (1 - n)) / (r - 1)
Man hätte als Variablennamen auch x nehmen können, statt r (angelehnt an das Wort "ratio").
Bei der Wahl des Iterationsstartwertes muss man vorsichtig sein, nicht mit jedem Iterationsstartwert konvergiert diese Formel. Beispielsweise mit den Startwerten r = 0 und r = 1 und r = - 1 gibt es keine Konvergenz.
Man kann aber getrost r = 2 als Iterations-Startwert verwenden.
Allerdings --> Je höher n ist, desto langsamer ist die Konvergenz, und desto mehr Iterationen werden benötigt.
Hier mal ein Bild :
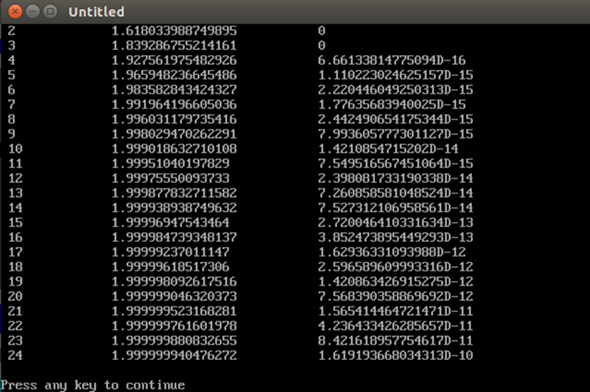
Die letzte Spalte kann man als Schätzwert für die Anzahl der Nachkommastellen hernehmem, die zuverlässig sind.
Man sieht auch, dass es insgesamt einen Grenzwert gibt, der gegen 2 strebt.
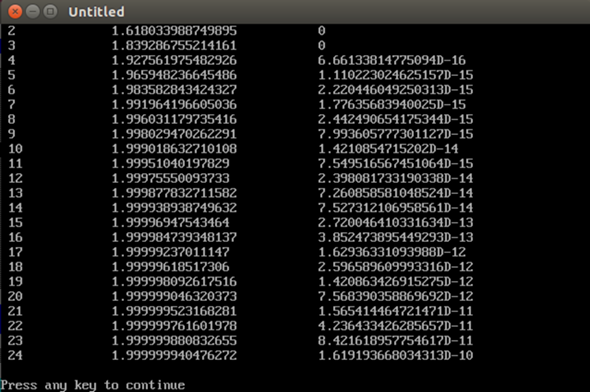
Ich hab das ganze ein wenig vereinfachen können:
Diese geometrische Reihe kann man ausrechnen und erhält nach ein wenig umformen:
Diese Gleichung scheint zu funktionieren, leider gibt sie aber immer auch 1 als Lösung aus. Jetzt muss das nurnoch weiter vereinfacht werden
Ich bin momentan der Meinung, dass man diese Gleichung nicht analytisch lösen kann.... (aber vlt gibt es auch einen coolen Trick)
Das hat mich auch gewundert, die anderen Zahlen sind aber trotzdem Lösungen, ich habe es schon mehrmals gecheckt, scheint alles richtig zu sein, weiss auch nicht wo die auf einmal herkommen
Die geometrische Summenformel kann selbst im kritischen Punkt x = 1 verwendet werden (mit l'Hospital lässt sich zeigen, dass der Grenzwert mit dem tatsächlichen Wert im Polynom übereinstimmt).... du hast danach alles auf einen Nenner gebracht und nur den Zähler = 2x^n-x^(n+1)-1 bei der Nullsetzung betrachtet (was sinnvoll war, da der Nenner dort keine Rolle spielt).
Nun hat der Zähler aber x = 1 als Nullstelle, was aber eigentlich keine Nullstelle des gesamten Quotienten (= 2x^n-x^(n+1)-1) / (1-x) darstellt.
(Siehe Grenzwert, z.B. berechnet mit Hilfe von der Regel von de l'Hospital)
Da du, wie vorhin bereits erwähnt, dich auf den Zähler konzentriert hast, hat sich also künstlich eine Nullstelle "dazugeschlichen"....
Fazit: Die Nullstelle bei x = 1 ist hier redundant und kann vernachlässigt werden.
Hoffentlich habe ich mich nicht vertan.
Schreib die Gleichung um zu
X^n = 1 + x + .... + x^(n-1)
Bzw.
X^n = (x^n - 1) / ( x - 1)
Bzw.
X^(n+1) - 2x^n + 1 = 0
Für große n kann man daran eine Lösung "nahe" 2 ablesen. Aber leider nicht als Formel.
Hier steht bei Wolfram was über die Reihen:
http://mathworld.wolfram.com/Fibonaccin-StepNumber.html
Für n=3 gibt es eine geschlossene Lösung, für größere n nicht mehr.
Für n=2 ist das Verhältnis der goldene Schnitt (3+sqrt(5))/2
Für n=3 spuckt Wolframalpha keine geschlossene Lösung mehr aus, dann ist das wahrscheinlich nicht mehr so einfach.
https://www.wolframalpha.com/input/?i=x%5E3++%E2%88%92x%5E2++%E2%88%92x%3D1
Eine real solution spuckt er schon aus, die komplexen kann man denke ich einfach ignorieren, ich habe es mal bis x^23 getestet und es gab immer reelle Lösungen, der Wert schien gegen 2 zu gehen
"real" ist nicht geschlossen. Die komplexen Lösungen sind irrelevant, ja.
Deine Umformung kann m.E. nicht stimmen, denn x=1 ist keine Lösung der Gleichungen in Deinem ursprünglichen Post.