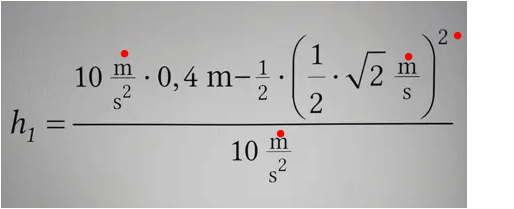
EINHEITEN WEGKÜRZEN?
Gezeigt wird eine Musterlösung. Ich verstehe aber nicht warum in der Lösung nur die Einheit (m) übrig bleibt.

5 Antworten
Im Zähler hast du die Einheit m²/s², im Nenner m/s².
gekürzt ergibt das eben m
Im Zähler ist die Einheit m²/s², wenn man das durch m/s² teilt, kommt m raus.
Das ist soweit logisch aber warum wird die Einheit m/s rechts im Nenner nicht berücksichtigt? Ach im Nenner findet eine Subtraktion statt deshalb bleibt es dabei danke für die Antwort.
Der Bruch nur mit den Einheiten würde lauten:
Im Zähler steht also m²/s², im Nenner m/s². Dabei kann man einmal m kürzen und 1/s². Übrig bleibt nur noch m.
Die eigentliche Frage wurde schon beantwortet. Allerdings ist die Musterlösung seltsam umständlich!
Der erste Teil ist einfach nur h(t)=h(0)-s(t) mit s(t)=Fallstrecke
Und s(t) ergibt sich aus s=1/2×a×t^2 und t=v/a, bzw t^2=v^2/a^2 mit a=g
dann ist s(t)=1/(2g)×v^2, was von h(0) abgezogen wird.
h(t)=h(0)-1/(2g)×v^2 würde vollkommen ausreichen!
Warum man das unbedingt auf einen Bruch bringen, erstmit g erweitern und dann doch wieder kürzen muss, ist mir vollkommen schleierhaft!
Im Zähler steht ein Summand
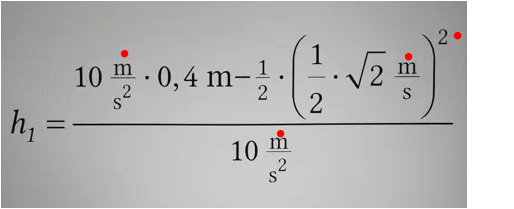
das minus jenem . In beiden Teilen ist ein m/s² vorhanden ( im hinteren wegen ()²)
das kürzt man gegen m/s² im Nenner . Übrig bleibt das m aus dem ersten Teil