Eine Welle zeichnen , aber wie?

Hallo Leute , ich verstehe echt nicht wie ich bei der folgenden Aufgabe vorgehen soll , um die Welle zeichenen zu können , Bitte helft mir ! Eine Querwelle schreite mit der Geschwindigkeit 2,5 m/s längs der +x-Achse fort. Der Erreger (x = 0) starte zur Zeit t = 0 seine Sinusschwingung mit f = 50 Hz und der Amplitude 2,0 cm. a)

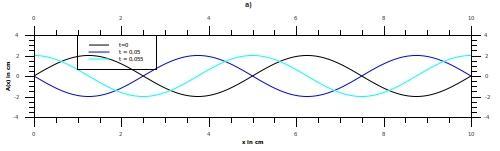
Zeichnen Sie die Welle zu den Zeiten t1 = 0,050s und t2 = 0,055s.

b)

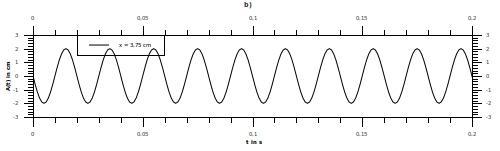
Zeichnen Sie das Diagramm der Teilchenschwingung am Ort x = 3,75 cm.

c)

Welcher grundlegende Unterschied besteht zwischen den Kurven bei a) und b)?

Answer 1

[Hyde4]

a) Wenn du also die Amplitude über dem Ort zeichnest, dann hast du zum Zeitpunkt t = 0 eine Welle, die bei (0/0) anfängt und deren Hochpunkt bei 2 cm ist und die eine Frequenz von 50 Hz hat, also 50 pro Sekunde, das heißt, die Wellenlänge beträgt: lambda = v/f = 0,05 m.

Bei t1 = 0,05 s hat sie sich einfach nur um die Strecke delta s = 2,5 m/s * 0,05 s = 0,125 m weiter nach rechts bewegt. Das sind 2,5 mal die Wellenlänge, also ist die jetzt genau entgegengesetzt, da wo vorher ein Maximum war, ist nun ein Minimum und andersrum.

Bei t2 dann eben nochmal weiter. Das ganze sieht dann so aus wie in meinem ersten Bild.

Als Gleichung heißt das:

A(x) = A0 * sin[kx-wt] = 2cm *sin[2 * pi * 50 1/s * (x/(0,025cm/s)-t)]

b) Hier nimmst du jetzt einen konstanten Ort x = 3,75 cm und zeichnest die Amplitude, also die Auslenkung in Abhängigkeit von der Zeit.

Du nimmst also dieselbe Gleichung, aber diesmal setzt du deinen Wert für x ein und lässt t als Variable, vorher haben wir t eingesetzt und x als Variable gelassen.

A(t) = A0 * sin[kx-wt] = 2cm *sin[2 * pi * 50 1/s * (3,75cm/(0,025cm/s)-t)]

= 2cm * sin[100 1/s * pi * (150 s-t)]

Das ist mein zweites Bild.

c) Der grundlegende Unterschied ist, dass a in Abhängigkeit vom Ort ist, also sozusagen die ganze Welle zu einer bestimmten festen Zeit zeigt, während b nur die Schwingung eines einzelnen Teilchens an einem festen Ort aber über die Zeit hinweg anzeigt. Das bei b ist nicht mehr die Welle selbst, sondern nur die Bewegung eines Teilchens in dieser Welle, das immer nur nach oben und unten schwingt. Daraus kann man noch mehr Schlüsse ziehen. Zum Beispiel den Unterschied zwischen Phasengeschwindigkeit und Schnelle der Welle erklären.