Ein regulärer Würfel wird dreimal geworfen.?
Folgende Aufgabe habe ich:
"Ein regulärer Würfel wird dreimal geworfen.
Wie groß ist die Wahrscheinlichkeit, dass dabei mindestens eine Drei geworfen
wird, unter der Bedingung, dass mindestens einer der Würfe eine Sechs ist?"
Das Ergebnis soll 30/91 sein, aber ich komme einfach nicht auf diese Lösung
Auf was für ein Ergebnis kommst du denn und wie ist dein Rechenweg dazu?
ich weiß dass die Wahrscheinlichkeit mindestens eine 6 zu Würfeln 1-/(5/6)^3 beträgt ich verstehe aber nicht wie ich die Bedingung jetzt genau in der Rechnung berücksichtigen muss
1 Antwort
Es gibt insgesamt 6^3=216 Möglichkeiten.
Davon sind 5^3=125 ohne 6, verbleiben 216-125=91 Möglichkeiten, mindestens eine 6 zu würfeln.
Es gibt 3! × 4 = 24 Möglichkeiten, um eine 6, eine 3 und eine aus {1,2,4,5} zu werfen. Dazu noch je 3 Möglichkeiten für 2 Sechsen und eine 3, bzw 2 Dreien und eine 6. Insgesamt also 30 für mindestens eine 6 und mindestens eine 3.
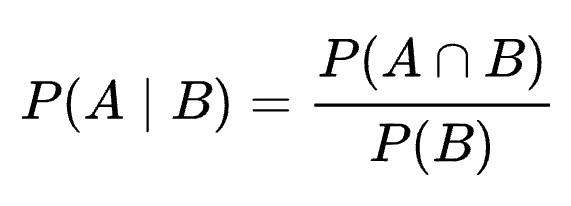
(Am Smartphone etwas fummelig)
Oben hast du 30/216, unten 91/216, also letztendlich die gesuchten 30/91.
Vermutlich geht das auch weniger umständlich 😉