Wie funktioniert das mit der Ebenengleichung in der analytischen Geometrie?
Hallo,
kann mir jemand bei dieser Aufgabe helfen bzw. erklären was ich machen soll (Mit Formeln & Rechenweg)?

Vielen Dank
2 Antworten
Die Konstruktion sieht so aus
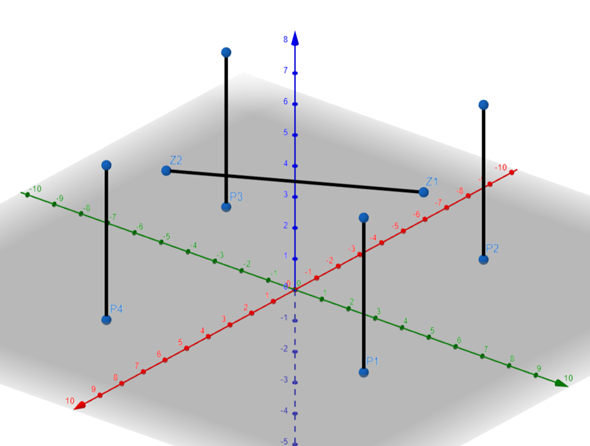
a)
Das ergibt aufgrund der Permutation der xy-Koordinaten.
b)
Länge :
d = Abstand der Punkte Z1 und Z2.
Winkel :
Den Richtungsvektor der Stange d = Z2-Z1 = (-2,8,1) bestimmen, und den Winkel mit dem Normalenvektor der xy-Ebene n = (0,0,1) über
sin(alpha)= (n x d) / (|n| * |d| ) bestimmen.
alpha ~ 6.91 Grad.
c)
Weil die Stange d und die Pfostenverbindungen P2#P3 bzw P1#P4 windschief sind.
d)
Um den Höhenunterschied der Stange in z-Richtung, d.h. genau 1 Meter. Denn dann verlaufen die Vektoren d und die Pfostenverbindungen P2#P3 bzw P1#P4 parallel.
e)
Richtungsvektor v von Z2 nach P3 (P3 mit z-Koordinate 5) bestimmen.
Richtungsvektor w von Z2 nach P4 (P4 mit z-Koordinate 5) bestimmen.
Winkel zwischen den beiden Vektoren v und w bestimmen, jetzt aber über
cos(alpha)= (v x w) / (|v| * |w| )
alpha ~ 128.25 Grad
oder
Richtungsvektor v von Z1 nach P1 (P1 mit z-Koordinate 6) bestimmen.
Richtungsvektor w von Z1 nach P2 (P2 mit z-Koordinate 6) bestimmen.
Winkel zwischen den beiden Vektoren v und w bestimmen, über
cos(alpha)= (v x w) / (|v| * |w| )
alpha natürlich wieder ~ 128.25 Grad
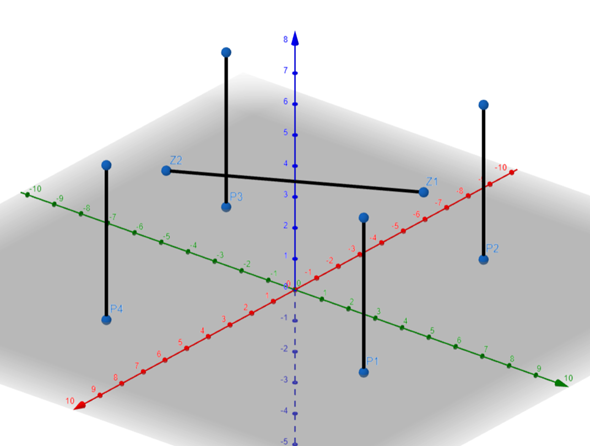
Bei a musst du einfach mit der Definition nachweisen, dass das entstehende polygon ein quadrat ist.
Vielen dank! :) Kannst du mir verraten wie du die Skizze so hinbekommen hast bzw welches Programm du benutzt hast?