Dielektrikum im elektrischen Feld?
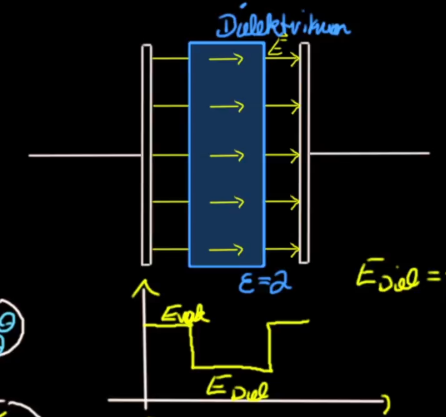
Ich verstehe warum das richtig ist, wenn wir einen metallischen Leiter in die Mitte des Kondensators bringen. Das Feld muss danach wieder gleichstark sein, weil der Leiter im inneren Ladungen so anordnet, dass er ein gleich starkes Feld entgegen setzt, damit das innere feldfrei wird.
Ist nun dieses Objekt, kein metallisches mehr, sondern ein nichtleitendes Dielektrikum, so verstehe ich, das es in den Atomkernen entsprechende Ladungsverschiebung gibt, die in Summe, schwächer sein soll, als das außenliegende E-Feld, sodass im Dieelektrikum das E-Feld bissl schwächer ist, als das äußere. Was ich dann aber nicht verstehe, warum danach wieder die ursprüngliche Feldstärke anliegen soll.
Quelle Bild: YouTube Video mit watchId: NdQmfcWCbSM
2 Antworten
Ich hoffe, dass ich deine Frage richtig verstanden habe und versuche es mal kurz zu erklären.
Bei einem Dielektrikum sind die Ladungen stärker gebunden auf der molekularen Ebene, sodass die Ladungen sich nicht frei bewegen können im Gegensatz zu einem elektrischen Leiter und das elektrische Feld sich nicht aufhebt durch Ladungsverschiebungen.
Die elektrische Feldstärke an einem Ort ist abhängig von dem Dielektrikum. Die Spannung hingegen ist nicht abhängig von der Dielektrizität, sondern wird durch die Potenzialdifferenz der Platten bestimmt. D. h. die Ursache der Feldstärke bleibt gleich, obwohl die Feldstärke unterschiedlich ist bei unterschiedlichen Dielektrizitäten.
Gerne :)
Aber ich würde es nicht als überlagert bezeichnen. Das wäre soweit ich weiß nicht korrekt.
Das elektrische Feld wird einfach durch die Dielektrizität beeinflusst bzw. hängt von ihr ab.
Die Formel der elektrischen Feldstärke zwischen zwei Punktladungen lautet wie folgt:
E = (Q_1 * Q_2)/(4*π*ε*r^2)
ε ist dabei die Dielektrizitätskonstante und ist dabei selber abhängig von einer Naturkonstanten und der relativen Dielektrizität des Stoffes.
Wenn die Dielektrizität sinkt, dann steigt der Wert der elektrischen Feldstärke. Wenn die Dielektrizität steigt, dann sinkt der Wert der Feldstärke. Die Feldstärke hängt also ab vom Material ab.
Da das Material nicht leitet, fällt eine angelegte Spannung über das Feld ab.
Dieselbe angelegte Spannung würde bei einem Leiter nun nicht mehr über ein elektrisches Feld abfallen, sondern über den Leiter selbst, weil ein Strom fließt und es auch kein E-Feld mehr gibt, da es durch die Leitfähigkeit des Leiters aufgehoben wird.
Man hat also bei derselben Spannung sozusagen 2 Arten wie die Spannung von einem Potenzial zum anderen abfällt. Einmal über ein E-Feld, wenn man den Zwischenraum mit einer Dielektrizität füllt. Und einmal über einen Leiter, wenn man einen Leiter dazwischen stellt.
Ich hoffe es ist so verständlicher ausgedrückt :)
Im Endeffekt lässt sich dieses Verhalten direkt aus der Materialbeziehung und dem elektrischen Fluss herleiten.
Und zwar gilt ja zunächst Q=Phi=D*A wobei D die elektrische Flussdichte im Kondensator ist. Da im Kondensator sich keine frei beweglichen Ladungen befinden muss D auch im gesamten Kondensator konstant sein. Eine Änderung von D würde ja bedeuten, dass freie Ladungen vorhanden wären was aber bei einem Dielektrikum ja global gesehen nicht der Fall ist.
Am Ende benötigt man also nur noch die Materialbeziehung D=epsilon*E bzw umgeschrieben E=D/epsilon.
Da D konstant ist muss E in jedem Bereich welcher mit dem selben Material gefüllt ist auch gleich sein.
Allerdings sei hier angemerkt, dass das einen Näherung für sehr sehr große Kondensatorflächen ist. Sobald man den Rand des Feldgebiets miteinbezieht stimmt das natürlich nicht mehr so ganz und die Form des Elektrischen Feldes wird durch das Dielektrikum verzerrt.
Danke dir. Das ist durchaus interessant dass der Raum diese Eigenschaft hat. Also obwohl das Feld scheinbar teilweise aufgehoben wird, geht es danach normalweiter. Es wird also zu keiner Stelle "eliminiert" sondern nur "überlagert".
Aber eigentlich nichts neues, lässt man in der Wellenlehre zwei Wellen aufeinander zulaufen, laufen diese nach dem Treffpunkt in Anfangsrichtung mit gleicher Amplitude weiter. Also von dem her bin ich zufrieden. Hat zwar nicht direkt etwas mit E-Feldern zu tun, aber naja.
Die Erklärung mit der Ursache ist einleuchtend.
Schönen Abend noch :)