bestimmen Sie den Inhalt dee gefärbten Fläche (Integral)?

Hallo,

ich bräuchte Hilfe bei diesen beiden Aufgaben.

Wäre nett wenn jemand mir helfen sollte, ich soll nämlich den Inhalt der gefärbten Flächen berechnen ^^

Comments

[Chrisslybear5]

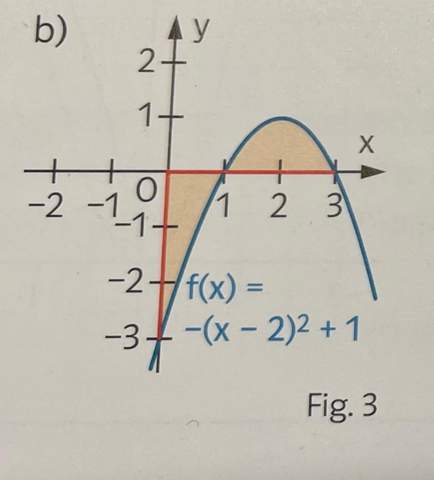
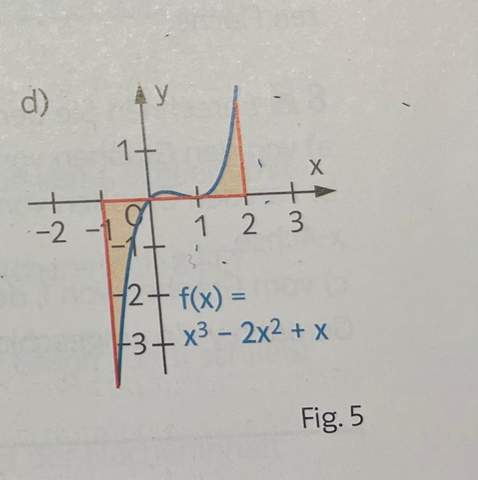
Hast du schon die Stammfunktionen berechnet?

[DuyDuyStein]

ich hab die stammfunktion für b, bin mir aber nicht sicher ob das so richtig ist

ich hab als stammfunktion:

(-(1/2x^2-2x)^2)dx…

Answer 1

[Rhenane]

Bzgl. der Stammfunktion multipizierst Du bei b) am Besten erst die quadr. Klammer aus und löst sie dann auf. Das macht das Integrieren einfacher (denn Dein "Versuch" in der Nachfrage ist falsch).

Dann integrierst Du die einzelnen Abschnitte separat, setzt die entsprechenden Grenzen ein und addierst abschließend die Beträge, d. h. die Ergebnisse der einzelnen Integrale ohne Minuszeichen, denn bei Flächen unter der x-Achse werden die Ergebnisse negativ sein. Hier brauchst Du die Beträge, weil es um Flächen geht, und die sind immer positiv.

Answer 2

[ztiromk]

Binomische Formel auflösen. Dann hast du:

$f\left(x\right)=-x^2+2x-4+1$ von da an integrieren ist leichter. So kannst du einfach die Regeln anwenden und kommst schnell auf

$F\left(x\right)\ =-\frac{x^3}{3}+2x^2-3x+c$ Grenzen Einsetzen schaffst du selbst ;) vergiss nicht auf die Nullstellen zu achten

Answer 3

[Dezin]

Bei Schritt 1 hast du ja schon angefangen: Stammfunktion berechnen.

Bei der ersten Funktion haben wir ja eine Verkettung der äußeren Funktion $u\left(x\right)\ =\ -x^2+1$ und der inneren Funktion $v\left(x\right)\ =\ x-2$ es gilt also f(x) = u(v(x)).

Um für diese Funktion eine Stammfunktion zu bilden, müssen wir zunächst die Stammfunktion U(x) für u(x) und die Ableitung v'(x) von v(x) berechnen.

Dann gilt:

$F\left(x\right)=\frac{U\left(v\left(x\right)\right)}{v'\left(x\right)}$

Schreib die Stammfunktion gerne in die Kommentare, dann können wir daran weiter arbeiten :)

Woher ich das weiß: Berufserfahrung – pädagogischer Assistent für Mathematik

Comments

[ztiromk]

Nein, das ist total unnötig. v(x) ist linear, das ist viel zu kompliziert gedacht.

[Dezin]

@ztiromk

"unnötig" würde ich nicht sagen. Ja, wir haben hier eine binomische Formel, die können wir auch auflösen. Allerdings geht das meistens nicht schneller und dieser Vorschlag wurde ja schon erwähnt :)

statt 1/v'(x) wird oft 1/m geschrieben (da v linear), ich denke aber nicht, dass das so viel einfacher ist und wir haben ein zusätzliches Formelzeichen, das wir erst einführen müssen...

Answer 4

[Halbrecht]

d)

du bestimmst die zwei Nullstellen

( 0 und 1 wahrscheinlich ) 

.

F(x) = 1/4 x^4 - 2/3 * x³ + 1/2 * x²

.

Drei !!! Integrale 

von bis

-1 0 

0 1 

1 2