Beispiel für eine Äquivalenzrelation bezogen auf die Symmetrie?
Hallo,
Ich habe dazu ein Beispiel gemacht. Stimmt er ?
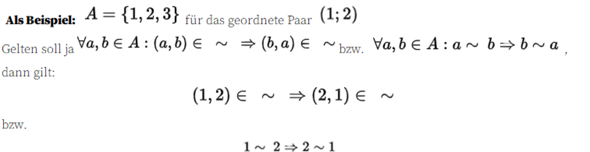
Wenn er stimmt, wie kann dann 1 äquivalent zu 2 sein und umgekehrt? Das sind doch nie im Leben Äquivalente Elemente zueinander.
3 Antworten
Das ist in diesem Beispiel so definiert: 1,2,3 sind in einer Äquivalenzklasse, daraus folgt zwingend, dass sie paarweise in Äquivalenzrelation zueinander stehen
man hätte auch Äpfel, Birnen und Kirschen statt 1,2,3 nehmen können
Wie nobytree2 bereits erwähnt hat, sind 1 und 2 in diesem Beispiel per definition äquivalent. Um das Beispiel zu vervollständigen: Eine Äquivalenzrelation auf {1,2,3}, bezüglich der 1 und 2 äquivalent zueinander sind, lautet z.B.
R = {(1,1), (1,2), (2,1), (2,2), (3,3)}.
Jetzt sagst du, dass 1 und 2 nie im Leben äquivalent zueinander sein können - aber das hängt eben davon ab, was du gerade als Äquivalenz betrachtest. Zum Beispiel:
Du interessierst dich dafür, ob du dich mit deinen zwei Kumpels in einem öffentlichen Park treffen darfst. Dies ist (hier zumindest) abhängig von der Corona-Stufe. Bei einer Stufe von 3 darf man sich nur mit zwei Haushalten treffen; bei einer Stufe von 2 mit drei Haushalten (ohne Test) und bei einer von 1 mit bis zu 5 Haushalten (ohne Test).
Da du und deine zwei Kumpels insgesamt drei Haushalte seid, dürft ihr euch nur bei einer Stufe von 1 oder 2 treffen. Aber welche dieser beiden Stufen es jetzt konkret ist, ist für euch unwichtig. Deswegen sind für euch die Stufen 1 und 2 gleichwertig (= äquivalent).
Wenn du jedem Element die Ausprägung einer Eigenschaft zuordnen kannst, sind alle Elemente, die bzgl. dieser Eigenschaft gleich sind, in der gleichen Äquivalenzklasse bzw. äquivalent.
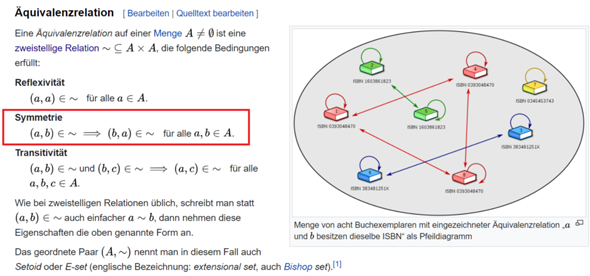
In deinem Beispiel ist die Eigenschaft "Farbe" und die Ausprägungen sind grün, rot, blau und gelb.
Ebenso kannst du ganzen Zahlen z.B. die Eigenschaft "Rest bei Division durch 7" zuteilen und hast anschließend 7 jeweils unendlich große Äquivalenzklassen. Dann ist z.B. 1 äquivalent zu 8 und 15 und 22 und ...