Aufgabe bedingte Wahrscheinlichkeit?
In dieser Aufgabe kann ich a) gut lösen und x bestimmen. Wie fährt man bei b) fort? Muss man hier einfach den Pfad A -> nicht-B gehen? Oder muss man hier irgendwie die Formel für die bedingte Wahrscheinlichkeit verwenden?
2 Antworten
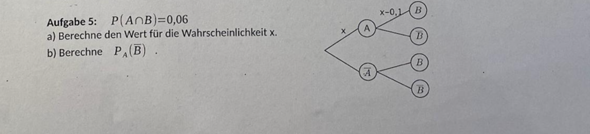
P_A(B-Strich) ist der Ast von A nach B-Strich. Und der muss zusammen mit dem von A nach B die Wahrscheinlichkeit 1 ergeben, d. h. P_A(B-Strich)=1-(x-0,1)=1,1-x. Und x hast Du ja schon bei a) ermittelt.
Kannst du die Wahrscheinlichkeit angeben, ohne x zu kennen?
Wenn nein, brauchst du den Satz von der bedingten Wahrscheinlichkeit und Auflösen des Gleichungssystems.
Das geht nur, wenn A und B unabhängig voneinander sind.
Da wir das nicht direkt aus der Aufgabenstellung entnehmen können, müssen wir dies ggf. prüfen, z. B. mit dem Satz der bedingten Wahrscheinlichkeit.
Und dazu wiederum müssen wir prüfen, ob
P(B) = P(A) P(B falls A) + P(nicht-A) P(B falls nicht-A)
es sieht so aus, als wenn hier mindestens eine Angabe fehlt.
Also bleibt nichts Anderes übrig, als uns auf den Teilbaum hinter (A) zu beschränken.
Da schöne quasi-ganzzahlige (max. 1 Nachkommastelle) Werte herauskommen, wenn (wie üblich) an den Ästen die Einzelwahrscheinlichkeiten stehen, gehe ich davon aus, dass
P(B falls A) = x - 0,1
ist.
Da wir uns innerhalb des Astes (A) befinden, ist
P(B falls Nicht-A) = 1 - P(B falls A)
Naja, x kann man ja aus a) ziemlich leicht ausrechnen. Aber was macht man denn nun bei b)?
Einfach P(A) * P(nicht-B)?