Altert man im Weltall langsamer?

Hallo ToxicYT,

die Frage...

Altert man im Weltall langsamer?

...ist falsch gestellt. Das Weltall ist sozusagen alles (einschließlich der Erde übrigens) mit höchst unterschiedlichen physikalischen Bedingungen.

Was das langsamer-Altern angelangt, so meinst Du damit sicher, dass Deine Uhren samt und sonders um einen bestimmten Faktor langsamer laufen als etwa auf der Erdoberfläche.

Auch dies kann man nicht pauschal sagen. Zweifellos lässt sich jedem Punkt |r> im Kosmos ein Gravitationspotential Φ(|r>) zuordnen. In diesem Potential hat sogar Licht, genauer gesagt jedem Photon der Frequenz f eine potentielle Energie

(1) E[pot] = h·f·Φ/c² (h Planck'sches Wirkungsquantum),

und die Summe aus dieser und der kinetischen Energie h·f ist konstant. Ändert sich also Φ, so ändert sich auch f, und zwar gegenläufig:

(2) f₂ = f₁(1 + Φ₁/c²)/(1 + Φ₂/c²).

Wenn ich jetzt bei |r>₁ eine Zeit Δτ lang einen Kaffee trinke und gleichzeitig Wellen mit der Frequenz f₁ erzeuge und abstrahle, und bei |r>₂ kommen die Wellen mit f₂ an, sieht der Vorgang bei |r>₂ u.U. länger oder kürzer aus, weil er in jedem Fall Δτ·f₁ Schwingungen dauert (Zahlen kannst Du nach belieben einsetzen, vorzugsweise sinnvolle).

Im Extremfall, von der engsten stabilen Kreisbahn (6μ-Orbit) um ein nicht rotierendes Schwarzes Loch (2μ ist der Schwarzschildradius) aus in den entfernten Weltraum ist der Faktor

(3) dt/dτ = 1/√{1 – v²/c² – 2μ/r} = 1/√{1 – μ/6μ – 2μ/6μ} = 1/√{½} = √{2}.

Dabei habe ich noch das Tempo v einbezogen, mit dem man in diesem Orbit unterwegs ist.

Hier ist eine Warnung angebracht: Oft wird auch im Zusammenhang mit Geschwindigkeit von 'Zeitdilatation' geredet. Das ist aber eigentlich Unsinn, denn Fortbewegung ist relativ - darauf beruht die Relativitätstheorie ja! Ihre flat-spacetime-Version ist schlicht die Anwendung von Galileis Relativitätsprinzip auf Maxwells Elektrodynamik.

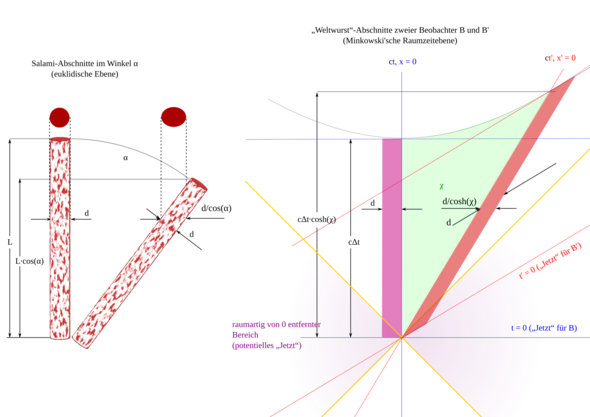
Es ist paradox, von einem 'Auseinanderziehen' der Zeit zu sprechen. Man redet ja auch nicht von 'Längenkontraktion' einer Salami, die man schräg an eine andere anlegt, die eigentlich gleich lang ist.

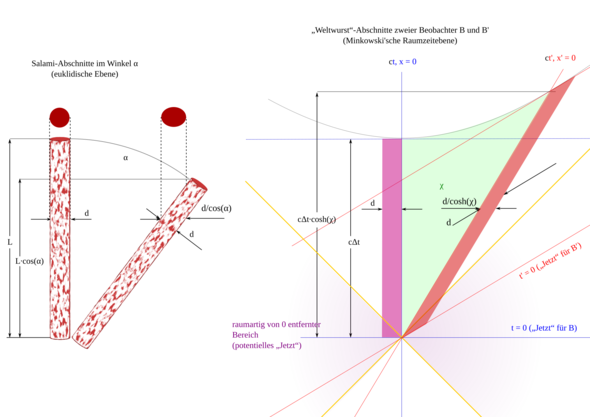
In der Raumzeit, zu der man Raum und Zeit zusammenzufassen hat, gibt es einen absoluten Abstand, der sich an räumliche Abstände anlehnt (Pythagoras), aber an einer Stelle ein Minuszeichen hat:

(4.1) Δτ := √{Δt² – Δs²/c²), falls cΔt ≤ Δs

(4.2) Δς := √{Δs² – c²Δs²), falls cΔt ≤ Δs

Dabei ist Δs ein räumlicher Abstand und Δt eine Zeitspanne zwischen zwei Ereignissen, jeweils in einem Koordinatensystem, von dem Δτ bzw. Δς aber unabhängig ist.

Daher sind gerade zeitartige Wege die längsten statt die kürzesten, und d.h. jemand, der wild im Weltraum umher reist, erlebt weniger Eigenzeit.

Es ist die Geschwindigkeit und Masse die die Zeit in Relation zur Erde langsamer macht. Wenn du an einem super massereichen Schwarzen Loch vorbei fliegst vergeht die Zeit für dich langsamer (1h an einem schwarzen Loch sind zum Beispiel 2h auf der Erde, der Zeit Unterschied ist nicht korrekt ich wollte es dir nur etwas verandchaulichen) mit einer hohen Geschwindigkeit ist dies auch der Fall. (Ich glaube mal gehört zu haben das wenn man 7 Tage mit 99.9 % Lichtgeschwindigkeit reist vergehen auf der Erde 100 Jahre)

Hallo ToxicYT,

nein. Warum sollte man?

Ich nehme an, Du verwechselst hier die Effekte der Relativitätstheorie...

Da gibt es das berühmte Beispiel für die Spezielle Relativitätstheorie, dass einer von zwei Zwillingen in ein Raumschiff steigt, eine große und schnelle Runde dreht... und sein Zwilling auf der Erde ist bei seiner Rückkehr ein alter Mann, während er selber noch recht frisch ist.

Nur: Dieser unterschiedliche Alterungsprozess kommt aus seiner Bewegung: Bewegte Uhren gehen langsamer. Er altert also langsamer, weil er sich bewegt, der andere Zwilling aber in Ruhe ist. Im Prinzip alterst Du auch langsamer als eine stehende Person, wenn Du aufstehst und im Zimmer rumläufst. (Die Effekte sind minimalst, aber berechenbar)

Das hat nichts mit dem Weltall zu tun.

Einsteins Allgemeine Relativitätstheorie beschreibt einen entgegenwirkenden Effekt: Uhren im Scherefeld gehen langsamer.

Weil im Weltall Schwerelosigkeit herrscht, alterst Du also sogar strenggenommen in einem Raumschiff, das relativ zu einem irdischen Beobachter in Ruhe ist (bzw. sich genauso bewegt) sogar schneller!

Auf der ISS oder in einem Flugzeug wirken sich also beide Effekte entgegen - die Uhr wird wegen der Effekte der Speziellen Relativitätstheorie etwas verlangsamt, wegen der Allgemeinen Relativitätstheorie etwas schneller relativ zu einer Uhr am Boden.

Auf der ISS - in rund 400 km Höhe - ist es so, dass die Effekte der Speziellen Relativitätstheorie minimal überwiegen: Astronauten, die Monate oben sind, sind gegenüber der am Beden gebliebenen Verwandtschaft wenige Sekundenbruchteile weniger gealtert.

Grüße

Nicht der Aufenthalt im All selber ist maßgebend, sondern das Beschleunigen auf hohe Geschwindigkeit.

Laut Einsteins Spezieller Relativitätstheorie ist die Lichtgeschwindigkeit die Grenzgeschwindigkeit im unserem Universum. Könnten wir lichtschnell fliegen (was aber unmöglich ist), würde die Zeit stillstehen. Es ist tatsächlich so, dass bei hoher Geschwindigkeit die Zeit langsamer abläuft (Zeitdilatation) und der Raumfahrer weniger schnell altert als der Erdbewohner. Dieser Effekt wurde auch durch Versuche mit zwei relativ zueinander bewegten sehr exakten Uhren bestätigt.

Es kommt darauf an, wo genau im Weltall man sich befindet.

Nur wenn, wo man sich befindet, das Gravitationsfeld stärker ist als auf der Erde, wird man dort langsamer altern. [ z.B. in der Nähe eines Schwarzen Lochs ].

Wer sich aber z.B. im freien Fall auf einer Umlaufbahn um die Erde befindet, wird dort etwas schneller altern als auf der Erde selbst.