Wieso teilt sich der Strom bei einem Kurzschluss nicht auf?
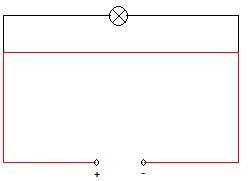
Hier auf dem Bild ein Kurzschluss. Wieso fließt der Strom hier nur über den kurz geschlossenen Leiter und teilt sich nicht auf und fließt somit auch durch die Lampe? Bei einer Parallelschaltung ist das doch der Fall, dass der Strom sich aufteilt und durch z. B. 2 Wiederstände fließt. Wieso fließt der Strom bei einem Kurzschluss NUR durch den Leiter anstatt sich aufzuteilen und durch den Leiter UND durch die Lampe zu fließen?
7 Antworten
Theoretisch hast Du vollkommen recht, da Leuchtmittel wie auch Kurzschlussleitung einen eigenen Widerstand haben. Praktisch ist dieser Unterschied aber i.d.R. so groß, dass über das Leuchtmittel kein nennenswerter Strom mehr fließt.
Beispiel: Glühlampe 60 W (Kaltwiderstand 65 Ω), Kurzschlussdraht 1 m x 1,5 mm²
Der Kurzschlussdraht hat einen Widerstand von 0,0119 Ω (1/56 Ω : 1,5), somit beträgt der Gesamtwiderstand 1 : (1/65 Ω + 1/0,0119 Ω) = 0,0118978 Ω.
Der Gesamtstrom bei 230 V beträgt (theoretisch) 19.331 A. Davon fließen über
- das Leuchtmittel 230 V : 65 Ω = 3,538 A (0,0183 %)
- den Kurzschlussdraht 230 V : 0,0119 Ω = 19.327 A (99,9793 %)
Der Anteil des Leuchtmittels ist also vernichtend gering und kann ignoriert werden.
Den habe ich absichtlich weggelassen, damit das Verhältnis deutlicher wird. Natürlich sind 19 kA Kurzschlussstrom im Hausanschluss unrealistisch.
Danke, guter Punkt. Die Leistung, die den Kurzschluß-Draht erhitzt, wäre 4.4 MegaWatt :-O
Ich weiß die Frage ist schon mehrere Jahre her aber würde die Lampe trotzdem bei voller Helligkeit leuchten ?
Wenn ich den Kurzschluss weglassen würde würden ja rechnerisch auch 3.538 A durch die Lampe laufen also müsste die Lampe bei voller Helligkeit leuchten egal ob Kurzschluss oder Leerlauf.
Erst einmal: Vorsicht mit Punkt und Komma.
Es sind ca. 3½ A gegenüber rund 19 kA.
Der tatsächliche Kurzschlussstrom beträgt im Haushalt bei einem B16-Automaten bis zu 80 A, bevor dieser sicher abschaltet. Entsprechend wären die o.g. Ströme umzurechnen.
Kurzschlussstrom:
80 A : 19.331 A · 19.327 A = 79,983 A
Leuchtmittel:
80 A : 19.331 A · 3,538 A = 0,0146 A
Die theoretische Leistung des Leuchtmittels beträgt demnach
P = U · I = 230 V · 0,0146 A = 3,368 W
Diese Leistung (5,6 % des Sollwertes) reicht nicht aus, um eine kalte 60W-Glühlampe zum Leuchten zu bringen.
Widerstand, es heißt Widerstand...warum schreibt ihr das immer verkehrt?
Der Strom sucht sich immer den kürzesten/leichtesten Weg, in diesem Fall also als Kurzschluss.
Wenn ich nun also einen 10 Ohm Widerstand und einen 20 Ohm Widerstand parallel schalten würde, würde der ganze Strom nur durch den 10 Ohm Widerstand fliesen weil das der leichteste Weg ist?? Das kann doch nicht sein, dann könnte man doch nie 2 Geräte parallel schalten es sei denn sie haben den selben Widerstand?
Das Verhalten eines Stromflusses kann man sich anhand eines Wasserflusses veranschaulichen. Bei + befindet sich eine Pumpe, die Wasser durch die Rohre (Leitungen) in Richtung - befördert. Das meiste Wasser wird durch solche Rohre fliessen, die keinen Widerstand bieten. Der einzige Widerstand ensteht durch den Rohrquerschnitt. Die Lampe ist eine Art Mühlrad. Weil das Wasser parallel zum Mühlrad ungehindert fliessen kann, wird sich das Mühlrad kaum bis gar nicht bewegen. Das würde sich erst dann ändern, wenn das parallele Rohr unterbrochen wird.
Weil ein der Leiter als ideeller Leiter einen Widerstand von null hat und die Lampe einen über 0. Deshalb fließen 100% durch die Leitung.
Aber halt nur wenn das ein idealer Leiter ist. In der echten Welt hat die Leitung einen (niedrigen) Widerstand und es fließt auch etwas Strom durch die Lampe.
Wenn Du + und - kurzschließt gibt es keinen Potentialunterschied mehr.
An der Lampe sind jetzt 0 Volt . Ohne Spannung kein Strom
Realistischer würde diese Rechnung, wenn man den Zuleitungswiderstand mit einbezöge :D