Wieso natürlicher Logarithmus von Null undefiniert?
Wieso hat man sich eine imaginäre Zahl i für die Wurzel von (-1) ausgedacht, aber keine für den natürlichen Logarithmus von Null? Welche Fehler würden dadurch entstehen?
Oder hat eigentlich x für lim(x)-->0 und x€R diese Funktion schon?
2 Antworten
Hab zwei anschauliche Bilder, wenn du scrollst.
Du denken ich zmd., verschmischst zwei Themen. Die imaginären Zahlen exisiteren um eine Erweiterung des reellen Zahlenraums zu bringen. So wie negative Zahlen wie -2 oder -15 eingeführt worden, um die natürliche Zahlen (1,2,3,4...) auf die Ganze Zahlen zu erweitern.
(In Koordinatensystem wie das was du unten siehst, sind imaginäre Zahlen oder deren Erweiterung, die komplexe Zahlen schlecht dazustellen (kann man, tut man aber nur im Studium).)
Das andere mit limes ist das Fernverhalten von Funktionen, und mit x aus R meinst du ja die reellen Zahlen. Also alle die man in der Schule macht. Hier kannst du Funktionen mit i oder so nicht darstellen.
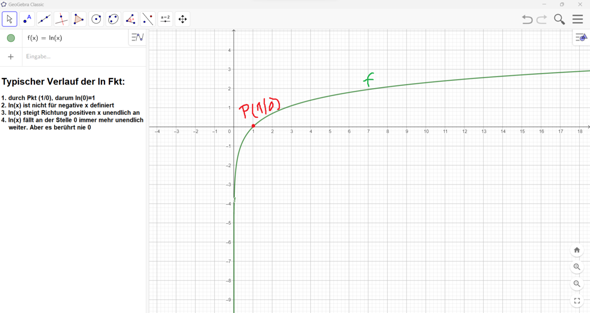
Anbei siehst du ja ein Bild von ln(x). Da verläuft sie so, dass sie bei x gegen 0 immer weiter ins negative Unendliche fällt. Allerdings kann sie nie 0 berühren, dafür ist sie schlicht nicht mathematisch definiert.
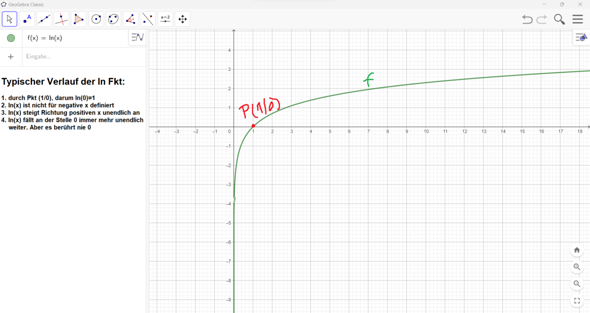
Für deinen gesuchten damit entstehenden Fehler: Würdest du es dennoch tun, bekämst du bei der Umkehrfunktion e ein Problem (die waren ja Quasi wie Tag und Nacht das Gegenteil voneinander).
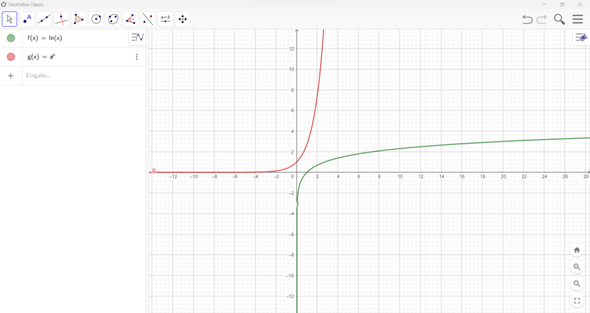
Die ist ja für f(x)=0 auch nicht definiert, wie sie mit x-> - unendlich sich immer mehr der 0 nähert aber nie berührt. [Siehe Bild 2]
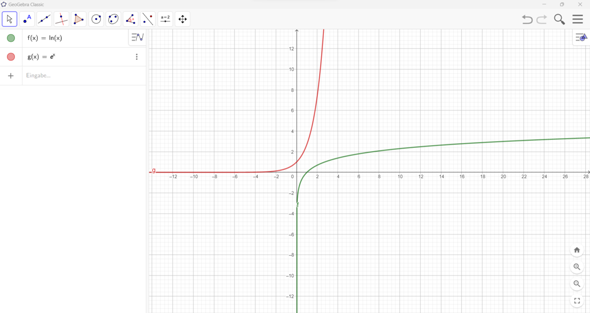
Es gibt ja bei e die Funktionsformel e^x. Aber egal was du für x einsetzt kann nie 0 rauskommen. Egal ob hoch e^1=2,7... e^0=1, e^-1= 1:e.
Solltest du aber bei den ln beschließen, dass der natürliche Logarithmus für 0 definiert ist, muss die Eulerfunktion es auch für F(x)=0. Das wäre ein mathematischer Fehler.
Man kann daher dafür keine Zahl sich ausdenken um diesen mathematischen Fehler zu beheben.
Der natürliche Logarithmus »hat« sozusagen den Wert minus unendlich. Dieser Wert ist nicht definiert, genauso wie der Wert der Funktion 1/x an der Stelle x = 0. Man kann aber durchaus den Grenzwert hinschreiben:
lim x -> 0 von log(x) = - unendlich.
Das Problem mit Unendlich ist, dass es keine normale Zahl ist. Man kann also nicht sinnvoll mit ihr rechnen. Denn unendlich + 1 = unendlich, sodass wir bei (1 + x) - x nicht mehr auf 1 kommen, wenn wir unendlich dort einsetzen würden. Wir hätten ein undefiniertes Ergebnis.