Wie rechne ich die möglichen Kombinationen aus?
Abend,
ich kann derzeit nicht einschlafen weil mich eine Frage in meinem Kopf daran hintert und ich die Kraft nicht habe diese zu lösen 😅
"Man hat einen Stapel unterschiedlicher Karten (x) und eine Fläche wo eine Anzahl an Karten platz hat (y). Wie könnte man die möglichen Kombination an Karten ausrechnen?"
Wenn wir davon ausgehen das x = 100 Karten sind und auf der Fläche y = 8 Karten Platz haben. Wie könnte man dies ausrechnen?
3 Antworten
stell dir die 8 Karten in einer Reihe vor .
dann gibt es
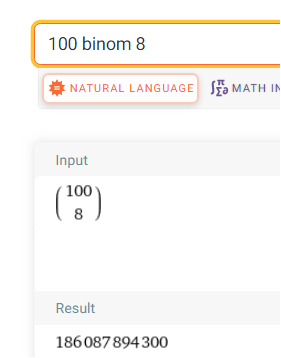
Möglichkeiten 8 Karten aus 100 auszuwählen
.
Und diese jeweils 8 Karten kann man wieder rum auf 8! = 8*7*6*5*4*3*2*1 Arten hinlegen
.
Jetzt schlaf schön und gib dem Teddy einen Bussi.
LG Halbrecht
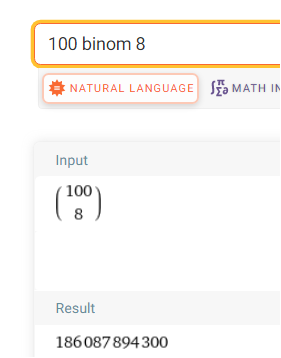
Das hängt davon ab, ob dieselben Karten in unterschiedlichen Anordnungen auf der Fläche als unterschiedliche Kombinationen gesehen werden oder nicht.
Wenn du jede Anordnung als eigene Kombination siehst, dann rechnest du wie folgt:
Es gibt 100 Möglichkeiten für das erste Feld, in jedem dieser Fälle bleiben danach weitere 99 Karten für das zweite Feld, danach 98 und so weiter, bis alle acht Plätze belegt sind.
Das heißt, es gibt 100 * 99 * 98 * 97 * 96 * 95 * 94 * 93 mögliche Kombinationen.
Wenn die Anordnung egal ist und es nur darum geht, welche acht Karten auf der Fläche liegen, musst du das Ergebnis der letzten Rechnung durch die Anzahl der Kombinationen teilen, die jetzt als identisch gelten.
Das sind all diejenigen, bei denen dieselben Karten auf dem Tisch liegen. Wie viele es davon gibt, ist leicht auszurechnen. Wir müssen wissen, wie viele Möglichkeiten es gibt, acht Karten auf acht Plätze zu verteilen.
Wir rechnen genau wie vorher 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1
Das Ergebnis der Rechnung oben teilen wir durch das Ergebnis der Rechnung unten. Man spricht hier auch vom Binominalkoeffizienten.
Wenn dich das Ergebnis der Rechnungen interessiert. Ich habe es für dich noch eben ausgerechnet.
Es sind 7.503.064.000.000.000 (gerundet auf Milliarden, weil die meisten Rechner nicht genauer sind) Möglichkeiten, wenn die Anordnung eine Rolle spielt.
Ist die Anordnung egal, sind es schon etwas weniger Möglichkeiten und zwar (diesmal genau)
186.087.894.300
Mehr als beim Lotto, wo es nur darum geht, 6 Zahlen aus 49 zu erwischen und nicht 8 Karten aus 100.
Wenn es auf die reihenfolge ankommt sind es 100*99*98*97*96*95*94*93 möglichkeiten