Wie löst man diese Aufgabe?
Ein Kochtopf hat eine kreisförmige Grundfläche mit einem Durchmesser von 24 cm. Er hat eine maximale Füllhöhe von 25 cm, ist jedoch nur zu 4/5 mit Wasser gefüllt. Wie viele Liter Wasser enthält der Kochtopf? (Achtung: 1 Liter = 1 dm³)
4 Antworten
Bei der Aufgabe muss man das Volumen eines Zylinders berechnen.
vermutlich ist dir die Formel fürs Zylindervolumen bekannt.
In diese Formel setzt du die benötigten Werte ein.
Durchmesser: 24 cm, der Radius ist 12 cm.
Die Höhe sind nicht 25 cm, sondern 4/5 davon. Das kann man schnell ausrechnen.
Achtung: 1 Liter = 1 dm³, wenn man diesen Tipp hat, sollte man die eingesetzten Werte von cm in dm umrechnen.
Dafür könnten dir folgende Erkenntnisse helfen:
Der Kochtopf ist ein Zylinder. Das Volumen eines Zylinders ist Grundfläche (das ist die Fläche der Kreise) mal Höhe.
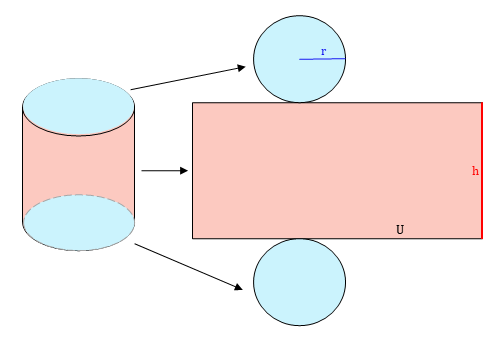
Der Radius r in einem Kreis ist die Hälfte vom Durchmesser d.
Die Fläche A eines Kreises lässt sich mit πr² = π(d/2)² berechnen.

1 dm = 10 cm
1 cm = 0,1 dm
1 dm³ = 1 l
Wenn die maximale Füllhöhe 25cm ist, er aber nur zu 4/5 gefüllt ist, ist die Höhe ja 4/5 von 25cm.


Ein Kochtopf hat eine kreisförmige Grundfläche mit einem Durchmesser von 24 cm. Er hat eine maximale Füllhöhe von 25 cm, ist jedoch nur zu 4/5 mit Wasser gefüllt. Wie viele Liter Wasser enthält der Kochtopf?
Wie löst man diese Aufgabe?
Man berechnet das Volumen des Wasserzylinders.
Eine Skizze kann helfen.
(Achtung: 1 Liter = 1 dm³)
Radius²×pe×höhe dann hast du das volumen und jetzt musst du nur noch ⅘ ausrechnen galub ich
⅘ sind 80 prozent jetzt musst du nur noch den dreisatz anwenden
Bei die Höhe habe ich nicht verstanden