Wie kann ich zeigen, dass die Seiten parallel sind?
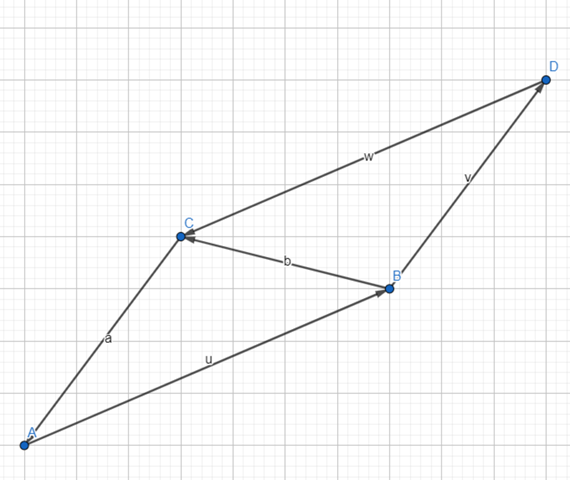
Ich muss bei folgendem Viereck zeigen bzw. erklären, dass die Seiten parallel sind. Wie soll ich das machen? Als Angabe habe ich folgende Koordinaten gegeben: A=(1(2); B=(8/5); C=(4/6) und D=(11/9). Ich habe die Koordinaten in Geogebra eingeben und habe ein Parallelogramm herausbekommen. Gibt es eine Möglichkeit, anders zu erklären, dass die Seiten parallel sind, ohne das Bild als Antwort einzufügen?
5 Antworten
Du könntest die Steigung zweier gegenüberliegenden Geraden berechnen.
Wenn sie die selbe Steigung haben, ist es ein Parallelogramm.
Ach ja und gegenüberliegende Winkel könntest du auch vergleichen. Wenn diese gleich sind, ist es auch ein Parallelogramm.
In dem du die Vektoren betrachtest, die die gegenüberliegende Seiten beschreiben.
Sind sie kollinear, dann sind die beiden Seiten Parallel
Vektoren: Kollinearität überprüfen.
Du hast die Koordinaten, daraus kannst du die Steigung
berechnen. Gleiche Steigung --> parallel.
Hi,
Aus den Angaben kannst du die Vektoren berechnen. Mit dem Richtungsanteil kannst du beweisen, daß die gegenüberliegenenden Seiten parallell sind.
M.E. einfacher ist es zu zeigen, daß die jeweils gegenüberliegenden Seiten gleich lang sind. Dann müssen die Seiten (im zweidimensionalen Raum) auch parallell sein.
m.f.G.
anwesende
Eigentlich ist das eine feste Eigenschaft von Rauten und Drachen.........
Aber mit den berechneten Längen könnte man mit Pythagoras die einzelnen Flächen Berechnen und beweisen, daß sich die beiden Diagonalen im rechten Winkel treffen und genau halbieren.
m.f.G.
anwesende
Wissen sie vielleicht auch, wie ich erklären kann, dass sich die beiden Diagonalen gegenseitig halbieren?