Wie kann ich ein Dreieck konstruieren?
Hallo,
Ich soll ein Dreieck konstruieren mit Seite B 4cm, Winkelhalbierende Gamma 5cm und Höhe C 3cm. Aber egal wie ich es versuche es gelingt mir (uns) nicht!
3 Antworten
Zeichne den Punkt A und die Gerade, auf der c liegt.
Parallel zu c zeichnest du eine Hilfsgerade im Abstand h_c (3 cm).
Von A aus schlägst du b (4 cm) auf die Hilfsgerade ab und erhältst C.
Von C 5 cm auf die Gerade, auf der c liegt abschlagen, den Schnittpunkt mit C verbinden. Dies ist die Winkelhalbierende von Gamma. den Winkel zwischen b und der Winkelhalbierenden verdoppeln, der Schnittpunkt mit der Geraden, auf der c liegt ist B.
Was mir seltsam vorkommt, ist, dass die Winkelhalbierende länger ist, als b.
Dachte ich mir.
Ich habs nur "im Kopf" gelöst und mir war klar, dass Gamma sehr groß sein muss. Habe auch vermutet, dass es kein solches Dreieck gibt.
wer etwas aufgepasst hat beim Pythagoras, kennt das geradezu antike Seitenverhätnis 3:4:5 als sogenanntes Pythagoreisches Tripel, also lauter ganze Zahlen als Seiten eines rechtwinkligen Dreiecks.
das mit der Winkelhalbierenden kann natürlich nicht stimmen
Hallo,
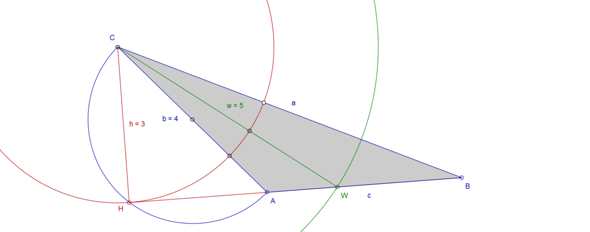
beginne mit Seite b (AC; 4 cm). Zeichne sie nach links geneigt.
Schlage um den Mittelpunkt von b einen Halbkreis (links, Thaleskreis).
Schlage um C einen Kreis mit dem Radius 3 cm.
Der Schnittpunkt dieses Kreises mit dem Halbkreis ist der Höhenfußpunkt H.
Er liegt außerhalb des Dreiecks.
Zeichne einen Strahl von H ausgehend über A ein.
Auf diesem Strahl liegt die Seite c.
Schlage um C einen Kreis mit dem Radius 5 cm.
Der Schnittpunkt dieses Kreises mit dem Strahl ist der Fußpunkt W der Winkelhalbierenden des Winkels gamma.
Verbinde C und W.
Verdopple den Winkel ACW.
Der Schnittpunkt des rechten Schenkels des verdoppelten Winkels mit dem Strahl ist der Punkt B.
Verbinde B und C.
Herzliche Grüße,
Willy
Hier hast Du noch die Konstruktionszeichnung:
Ich habe mal versucht, das Ding mit diesen Maßen zu konstruieren. Kannst Du vergessen. Danach hätte Gamma mehr als 180°.
Ich habe mit der Seite b angefangen und dann die Höhe über den Thaleskreis und den Radius 3 cm konstruiert. Aber Deine Methode klappt auch.