Wie hoch ist die Ausfallwahrscheinlichkeit der Maschine?
Eine Maschine hat 2 wichtige Bauteile.Fällt ein Bauteil aus,so ist die Maschine kaputt.
Bauteil 1 fällt in der Zeit 1000 Stunden mit 10% Wahrscheinlichkeit aus.
Bauteil 2 fällt in der Zeit 1000 Stunden mit 20% Wahrscheinlichkeit aus.
Wie hoch ist die Wahrscheinlichkeit,dass die Maschine in dem Zeitraum von 1000 Stunden kaputt geht ?
2 Antworten
Machs über das Gegenereignis, also dass beide Bauteile ganz bleiben. Beim ersten Bauteil ist diese Wahrscheinlichkeit 90% und beim zweiten 80%.
Das heißt, die Wahrscheinlichkeit, dass beide ganz bleiben ist 0,90*0,80 also 0,72 oder 72%. Das heißt, die Wahrscheinlichkeit, dass mindestens ein Bauteil kaputt geht ist 100% - 72% also 28%.
Angenommen es wären 5 Bauteile, jedes geht mit 20% Wahrscheinlichkeit kaputt. Ist die Wahrscheinlichkeit, dass die Maschine kaputt geht, dann 5*20% also 100%?
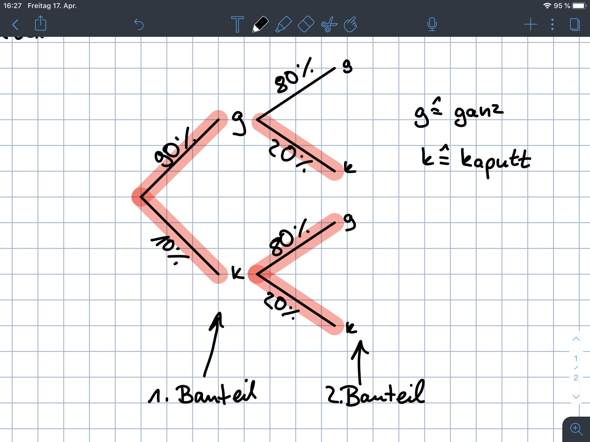
Hab dir hier mal das Baumdiagramm gezeichnet. Rot markiert sind die Pfade, die dazu führen, dass das Gerät kaputt geht.

Fehlen da nicht noch Pfade ?
Pfad 1 90% → 20% kaputt
Pfad 2 80% → 10 % kaputt fehlt
Pfad 3 10 % → ..... kaputt
Pfad 4 20% → ... kaputt fehlt
Es müßte dann noch weitere 2 Pfade geben.
Wie wird denn das Ereignis (Maschine kaputt) dann berechnet ,wenn Teil 1 oder Teil 2 ausfällt,dann speilt es doch keine Rolle mehr,wenn das restliche Teil nicht kaputt geht ?
Es spielt sehr wohl eine Rolle. Die Wahrscheinlichkeit für das Ereignis „Maschine kaputt“ ist die Summe der Einzelwahrscheinlichkeiten für „Kaputt-Ganz“, „Ganz-Kaputt“ und „Kaputt-Kaputt“. Welche Pfade da deiner Meinung nach fehlen, verstehe ich leider nicht ganz...
Mir ist da eine Idee gekommen.
Es gibt den Begriff der "Verfügbarkeit"
Beispiel:Man fährt mit dem Auto nach München und dazu sind die 4 Räder notwendig.
Fällt nur ein Rad aus,dann kommt man nicht nach München
Wahrscheinlichkeit,dass ein Rad nocht audfällt P(Rad)=0,99
Die Verfügbarkeit berechnet sich dann
P(Verfügbar)=0,99*0,99*0,99*0,99=0,99⁴=0,96... also 96%
Mit einer Sicherheit von 96% kommt man dann in München ohne Panne an.
Da Selbe gilt dann auch für diese Maschine.
Wahrscheinlichkeit,dass di Maschine 1000 Stunden läuft
P(läuft)=0,9*0,8=0,72 → 72%
P(kaputt)=1-0,72=0,28 → 28% Wahrscheinlichkeit,dass die Maschine in den 1000 Stunden kaputt geht
Deine Rechnung ist damit richtig.
Weiter habe ich gerechnet
Pfad 1 P(1)=0,9*0,2=0,18 kaputt
Pfad 2 P(2)=0,8*0,1=0,08 kaputt
P(1,2)=0,18+0,08=0,26
weiter
Pfad 3 P(3)=0,1*0,2=0,02
P(3) zuerst fällt Teil 1 aus → Maschine wird repariert,dann fällt Teil 2 aus
Addiert P(kaputt)=P(1)+P(2)+P(3)=0,18+0,08+0,02=0,28 → 28 % Wahrscheinlichkeit,dass die Maschine ausfällt.
Bekommst von mir auf jeden Fall die höchste Auszeichnung.
Wie so kann man das nicht über die 2 Pfade machen
Pfad 1 P(1)=0,1 → 10% Wahrscheinlichkeit,dass Teil 1 kaputt geht
Pfad 2 P(2)=0,2 → 20% Wahrscheinlichkeit,dass Teil 2 kaputt geht
als Summenregel → Teil 1 geht kaputt oder Teil 2 geht kaputt
Gesamtwahrscheinlichkeit dann P(ges)=P(1)+P(2)=0,1+0,2=0,3 → 30 % Wahrscheinlichkeit,dass die Maschine kaputt geht.
Sind aber 2 verschieden Ergebnisse.
Wo ist der Fehler ?