Wie gibt man die Symmetrieachse an und berechnet diese bei Parabeln/Quadratische Funktionen?
Hallo, ich schreibe morgen eine Mathe Arbeit und habe leider keine Ahnung wie man das macht? Ich bitte um schnelle Antworten
1 Antwort
Eine Parabel kann achsensymmetrisch zu einer Achse sein. Im Normalfall ist diese Achse bei einer Parabel die y-Achse. Wird der Graph bzw. die Funktion jedoch verschoben, verschiebt sich auch die Symmetrieachse.
Die Symmetrieachse geht durch den Scheitelpunkt der Parabel und ist somit auch genau in der Mitte der beiden Nullstellen. Sofern nur eine (doppelte) Nullstelle vorliegt, ist diese Nullstelle bereits der Scheitelpunkt, wo auch die Symmetrieachse durchgehen muss.
Beispiel 1:
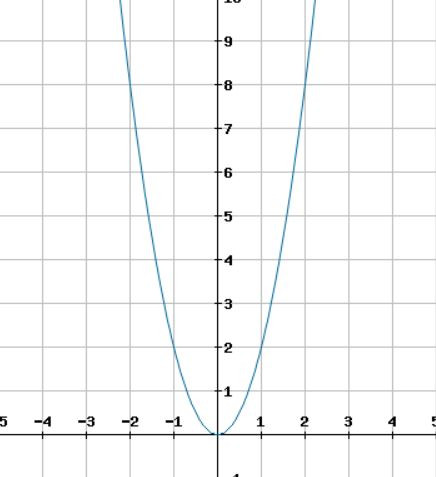
f(x) = 2x²
Die Symmetrieachse ist die y-Achse, weil die Parabel ihren Scheitelpunkt sowie die Nullstelle genau im Ursprung hat:
Beispiel 2:
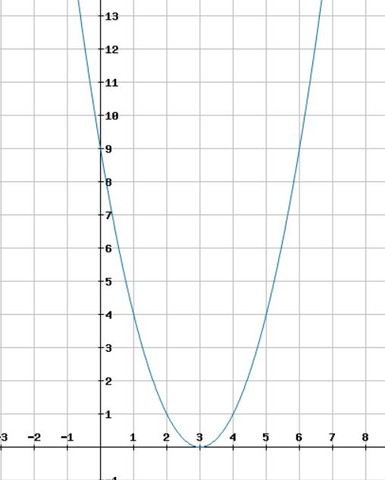
g(x) = (x-3)²
Hier der Graph der Funktion g:
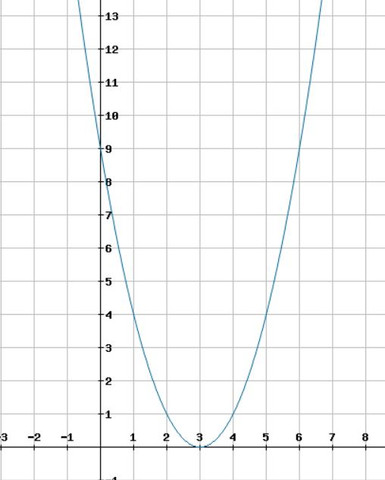
Die Parabel ist nun um 3 LE nach rechts verschoben. Demnach verschiebt sich auch die Symmetrieachse um 3LE nach rechts. Die Funktiongleichung der Symmetrieachse lautet nun: x = 3. Das wäre also eine senkrechte Gerade, quasi die y-Achse nur 3 LE nach rechts verschoben.
Beispiel 3:
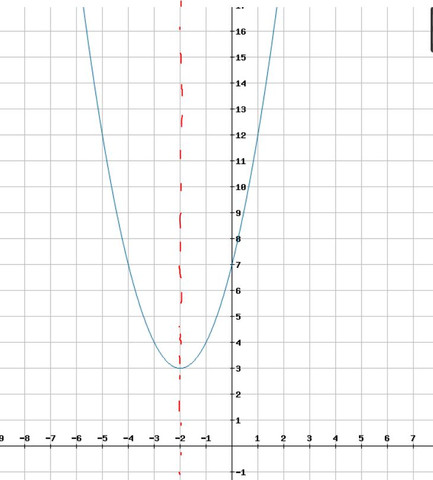
h(x) = (x+2)² + 3
Hier der Graph der Funktion h:
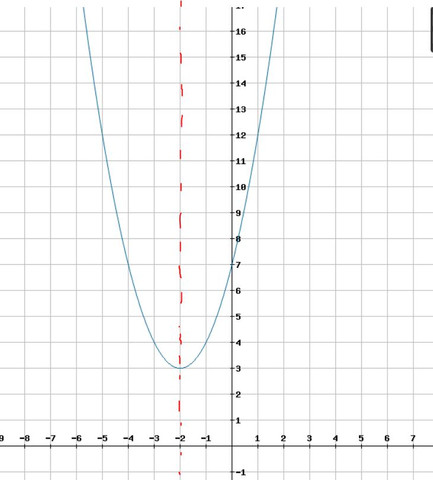
Die Symmetrieachse ist bereits eingezeichnet. Sie hat die Gleichung x=-2.
Liebe Grüße
TechnikSpezi