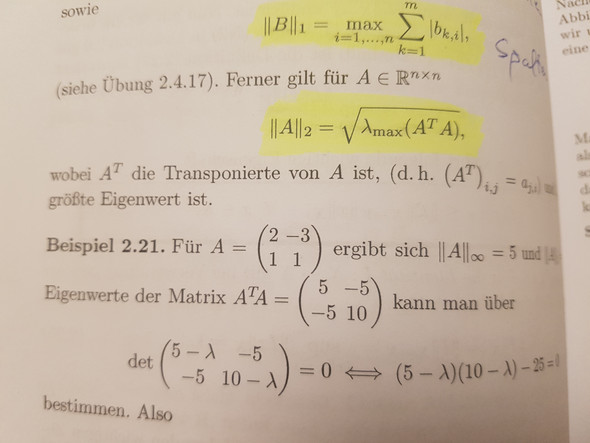Wie berechnet man die zweinorm der Diagonalmatrix von A?
Punkt 10.. ich kann mir nicht vorstellen, dass man das so ausrechnen muss.. da muss es einen trick geben
3 Antworten
Man kann sich auch fragen, was die Matrix D eigentlich mit A zu tun hat. Vergleich mit meinen (alten) Numerik-Notizen liefert, dass D diejenige Diagonal--Matrix ist, deren k-tes Diagonal Element gleich den reziproken Wert des betragsgrößten Elements der k-ten Zeile der Matrix A hat. Wenden wir diese Definition an, so finden wir D = diag(1/4,1/4,1/2). Die 2--Norm von D berechnet sich leicht: ||D||_2 = (3/2)^(1/2)/2. [Ich weiß nicht, wie ihr die 2-Norm definiert habt, vmtl. aber über ||D||_2'=min_{k}(\sum_{j=1}^n |A_{kj}|^2)^(1/2).
Die zweinorm einer matrix haben wir als sqrt(lambda_max(A*A^T)) definiert. Das ist aber ein enormer Rechenaufwand für so eine kleine Aufgabe. Erst A mal A^T ausrechnen. Dann die eigenwerte davon bestimmen. Und dann die wurzel des größten eigenwertes.. das kann doch nicht sein
Ich komme aber bei der zweinorm für die diag matrix auf sqrt(0.5*0.5)=0.5
Du musst nicht ||A|| berechnen, sondern ||D||.
Wieso da jetzt 0,25 und nicht 4 raus kommt versteh ich jedoch leider nicht. Allerdings weiß ich auch nicht was mit „Zeilenskalierung“ gemeint ist.
D ist nicht angegeben nur A und ich weiß nicht wie ich schnell auf D kommen kann
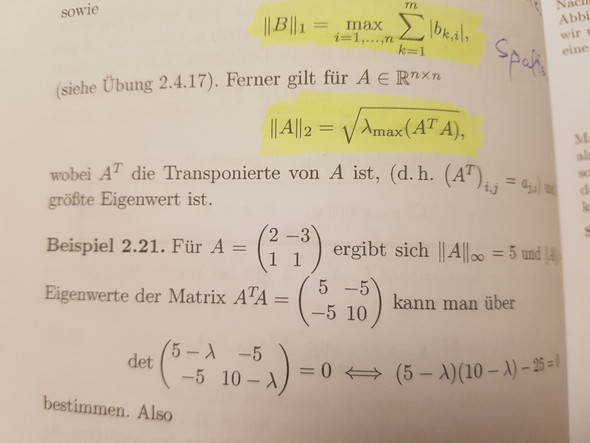
Die zweinorm der matrix. Ist vom buch Numerik für Ingenieure und Naturwissenschaftler von W. Dahmen A. Reusken. Auf dem Buch baut unsere Vorlesung auf.
