Wer kann dieses spassige Matherätsel für die ganze Familie lösen😂😂?
Nur 2%!! einer koreanischen Hochschule konnten dieses Rätsel lösen 😔😳😳😳😳
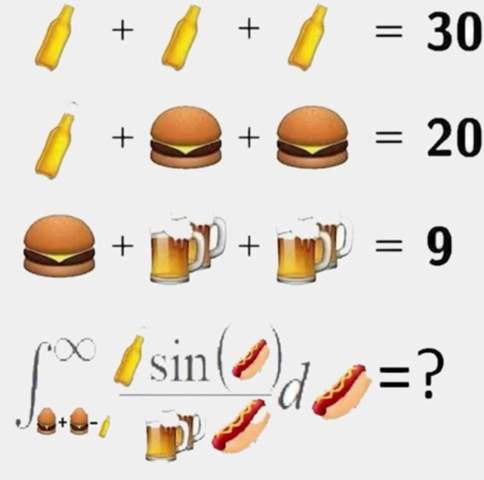
Wer bekommt es gelöst? 😵🧐🙊🙊
9 Antworten
Müsste
sein
https://de.wikipedia.org/wiki/Integralsinus
lim_{x->unendlich} si(x) = pi/2
Weil integral sin(x)/x <=> integral si(x) folgt, dass das Ergebnis 5pi/2 sein muss
Ja, jetzt hab ichs auch gesehen. Das ist mir fast schon unangenehm.^^
Das ich das falsch gesehen hab, dass das keine 8 sondern eine 0 ist.
a+a+a=30 => a=10
a+b+b=20 => b+b=20-10 => b=5
b+c+c=9 => c+c=9-5 => c=2
Integral(b+b-a;oo) = Integral(0,oo) (a * sin(x)) / (c * x) dx =
Integral(0,oo) (10 * sin(x)) / (2 * x) dx
Das ist 5* der Intergralsinus(oo) und das ist 5 * pi/2 = ca. 7,8539816
aber wer von der ganzen Familie kennt schon den Integralsinus ?
Löse zunächst das lineare Gleichungssystem der ersten drei Gleichungen. Setze die Lösung dann in das Integral ein und berechne.

Bei (*) habe ich einfach den Wert π/2 auswendig im Kopf gehabt. Das Integral ist gar nicht soo einfach zu berechnen, wenn man stur versuchen würde eine Stammfunktion zu finden. Stattdessen hilft beispielsweise eine Laplace-Transformation oder ein Abstecher in die komplexen Zahlen.
Siehe auch:

Linearer Faktor 5 kann man herausziehen. Integral von sin (Hotdog) / Hotdog über 0 bis unendlich ist pi/2 (https://de.wikipedia.org/wiki/Integralsinus). Lösung ist 5/2 pi.
Können schon. Aber die Lust Integrale um Viertel nach 12 außerhalb der Prüfungszeit zu lösen hält sich doch stark in Grenzen.
Wie kommts du denn darauf? Da steht doch effektiv 5sin(x)/x in den Grenzen von 8 bis unendlich.