Welcher Graph gehört zu welcher Funktionsgleichung??
Hi, ich soll folgende Aufgabe lösen: Welcher Graph gehört zu welcher Funktionsgleichung? Begründe deine Entscheidung. Wir haben das Thema heute neu in der Schuld gemacht, ich bin aber ziemlich orientierungslos wie ich hier vorgehen soll. Es ist sicherlich eine ziemlich leichte Aufgabe, daher will ich nur wissen, wie ich erkenne, was richtig ist. Ich danke jedem für Hilfe. Es geht um nr2.
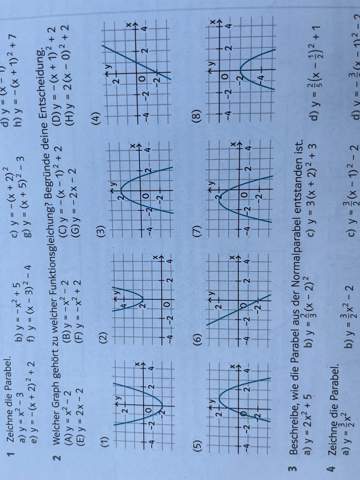
2 Antworten
-Geraden haben kein x im Quadrat, sondern nur Parabeln/Normalparabeln
-Wenn vor dem x im Quadrat ein Minus steht, ist sie nach unten geöffnet (negativ). Wenn kein Minus davor steht, ist sie nach oben geöffnet (positiv).
-Steht vor dem x im Quadrat z.B. ¼, dann ist es keine Normalparabel, sondern eine Parabel. Parabeln sind breiter/schmaler als Normalparabeln.
-In z.B. x(im Quadrat)+3 ist die 3 der Y-Achsenabschnitt. Da hier ein Plus davor steht, liegt der Punkt 3 der (positiven) Y-Achse auf der Parabel.
PS: In (C), (D) und (H) ist die Gleichung nicht in der Normalform, sondern in der Scheitelform. Von der Scheitelform aus wechselst du entweder zum Scheitel (mit dem man auch Parabeln/Normalparabeln bestimmen kann) oder in die Normalform.
Hoffe das hilft.
LG Salty
Edit: Hier sind übrigens die allgemeinen Funktionsgleichungen wie ich sie kenne:
-Normalparabeln haben die Funktionsgleichung y=x(im Quadrat)+bx+c.
-Parabeln haben die Funktionsgleichung y=ax(im Quadrat)+c. C steht für den Y-Achsenabschnitt.
-Geraden haben die Funktionsgleichung y=m•x+c. M steht für die Steigung, die bekommt man über die Formel m= y1-y2/x1-x2 (das / ist ein Bruchstrich, das Ganze muss im Bruch stehen) oder über das Steigungsdreieck.
Habe nur noch eine Frage wie es dann bei der (7) ist. Es gibt ja nirgends +1. das verstehe ich noch nicht. Oder ist die Schnittpunkt egal?
Bei der (7) kann man den Schnittpunkt ablesen über die Symmetrie. Dieser liegt bei S(x|y) = S(-1|2). Du kannst jetzt damit von der Scheitelform in die Normalform und mit den anderen Gleichungen vergleichen.
Hallo GrubHertha,
einen Teil kannst du an dem y-Achsenpunkt ablesen. Dann schaust du dir nur noch die Steigung an.
Viele Grüße
Vielen Dank, es hilft sehr.