Was ist der Unterschied zwischen dieser und der Sinus-Kurve?
Ich habe leider vieles, wegen meiner OP verpasst. Kann mir jemand die Eigenschaften und die Unterschiede zwischen dieser und der normalen Sinus Kurve nennen? Und woher man das wissen kann.
Bitte aufrichtig um Verständnis und Hilfe.
Gruß.
4 Antworten
Eine Sinuskurve zeichnet sich durch
die Amplitude: Ausschlag in Y-Richtung
Frequenz: Anzahl der Schwingungen in X-Richtung in einem bestimmten Intervall
Offset: Verschiebung des Nulldurchgangs (Schnittpunkts mit der x-Achse) in X-Richtung aus. Außerdem kann die Sinuskurve auch noch auf der Y-Achse verschoben sein.
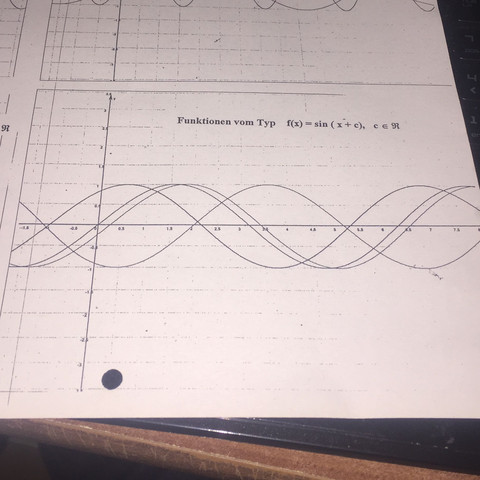
Bei deinem gezeigten Beispiel stimmen die drei Kurven in Amplitude und Frequenz überein.
Der einzige Unterschied liegt in der Position des Nulldurchgangs in X-Richtung. Eine Kurve schneidet die x-Achse bei 0 (hier ist c=0), eine andere bei x=0,25 (hier ist c=-0,25) und die letzte bei x=-1 (hier ist c=1).
Beantwortet das deine Frage?
Moin,
zu deiner Frage... es sind 3 Sinuskurven und du sollst herausfinden wie die Formel für diese ist.
Wie auf deinem Blatt steht ist die allgemeine Formel für eine Sinusfunktion
F(x)= a sin(bx+c)+d bei dir ist es nur f(x)= sin(x+c) was ich dir sofort erkläre:
Eine Sinusfunktion hat bestimmte Eigenschaften die durch die Variablen beschrieben werden...
a= (auch oft) A= Amplitude dies beschreibt die maximale Ausdehnung der Funktion. Wie du bestimmt weißt ist es egal was innerhalb von sin(x) steht der Wert ist immer im Intervall [-1,1]. Wenn man nun ein bestimmtes A hat kann man diesen Wert erhöhen.
b= ist ein Faktor der Frequenz,
c= ist ein Faktor der die Schwingung (Sinusfunktion) schon anhand des Graphen verschiebt
d= Die übliche Konstante in Formeln um den Graphen nach oben zu verschieben.
Einmal ein Bsp: F(x)=2 *sin( (pi)*x)+2
Wie würde die nun aussehen?
Erstmal merkt man, dass die Funktion um 2 nach oben verschoben ist und eine Amplitude von 2 besitzt. Daraus folgt die Kurve verläuft zwischen gedachten Linien die parallel zu der x-Achse sind in Höhe von 0 (x- Achse) und 4. (2-2 und 2+2)
Nun ist sie wenn wenn du Zahlen einsetzt schon bei x=2 "einmal durch", dh. sie hat einmal ihre ganze Bewegung durchgeführt und macht die Selbe jetzt immer wieder.
Eine Normale Sinusfunktion wäre erst bei x=2pi einmal so durch. Diese ist bei x=2pi schon über 2x(!) durch. Dh die Frequenz ist höher.
Nun zu deinen Aufgaben: Wie dir auffällt sind alle 3 Kurven zwischen 1 und -1 also ist die Amplitude 1 und d=0 (d= (max Wert +min Wert)/2) und alle verlaufen Parallel daher haben alle ein gleiches b. Was fehlt noch?
Genau c. dieses sollst du bestimmen.
Am einfachsten geht es wenn du dir anguckst wo die Funktionen die y-Achse schneiden (da x hier ja 0 ist) folgt das man nur sin(c) berechnet.
Also ist das jeweilige c=sin^-1(Y-wert bei 0)
hoffe dass ich helfen konnte
mfG Henri
Natürlich!
Also x ermittelst du in dieser Aufgabe nicht ^^ Daher fällt es jetzt mal weg, da es einfach die übliche Laufvariable ist.
Wie bekommt man c:
Du siehst das all die Graphen die y-Achse in verschiedenen Höhen durchlaufen oder?
einmal bei ca -0.25 einmal bei 0 und einmal bei ca 0,75.
Nun sind wie in meiner vorherigen Erläuterung geschrieben a,b,d klar. Also hat es nur was mit c zu tun.
Stell dir vor du hast eine Funktion der Form f(x)=sin(bx)... Egal was du für b einsetzt gilt immer: f(0)=0 Also hat diese Höhe was mit c zu tun.
Um dieses zu ermitteln nutzen wir gerade diese Eigenschaft der Kurve... Wir berechnen jedes mal f(0) nur das diesmal gilt
f(0)=sin(0+c) (die 0 lassen wir im folgendem weg) Also:
f(0)=sin(c) Und was ist f(0)? Es ist der Wert den deine Funktion bei x=0 hat also genau der Punkt an dem der Graph die y-Achse schneidet. Also in diesem Fall gilt
1) 0=sin(c)
2)-0,25=sin(c)
3)0.75=sin(c)
Jetzt musst du die Umkehrfunktion von sin benutzen um c zu bekommen (sin^-1). Keine Sorge hat dein TR.
Nun zur Amplitude: Ich sage es mal salopp:
Du siehst das die Kurve Punkte hat die max hoch bzw max tief sind?
Es geht erst hoch bis zu einem bestimmten Punkt und dann runter bis zu einem bestimmten und das immer wieder zu den Selben!
Nun guck dir an wo diese Punkte sind. Berechne nun [H(max)-H(min)]/2 in diesem Fall [1-(-1)]/2=2/2=1
Hallo,
die Funktionsgraphen von f(x) = sin(x) und g(x) = sin(x+c) sehen gleich aus.
Der Unterschied besteht darin, dass der Graph von f horizontal um c Einheiten nach links verschoben ist, wenn c positiv ist, und nach rechts verschoben ist, wenn c negativ ist.
Z. Bsp. wird durch Verschieben um π/2 (entspricht 90°) nach links aus der Sinuskurve die Cosinuskurve: sin(x+π/2) = cos(x).
Du kannst dich über das Thema informieren, wenn du nach "Verschieben von Funktionsgraphen" suchst.
Hier ist eine Seite, von einem Schüler gemacht:
http://rmg.zum.de/wiki/Facharbeit_Florian_Wilk/Verschieben_von_Funktionsgraphen
Gute Besserung und willkommen auf GF!
Kannst du mir nochmal erläutern wie ich c und x ermittle und wie ich die amplitude ablesen kann?