Was bedeutet symmetrisch zur y-Achse?
Hallo. In der Steckbriefaufgabe steht: eine Funktion vierten Grades ist symmetrisch zur y Achse und hat im Punkt p (2/0) eine Wendetangente mit der Steigung m= -4/3
Aber was bedeutet symmetrisch zur y Achse? Welche Bedingung ergibt sich daraus? Danke :-)
5 Antworten
Ein Punkt aus deiner Steckbriefangabe lässt sich doppelt verwenden. Bekommst du den Hinweis, es gebe einen Punkt (4| 7), dann gibt es bei Achsensysmmetrie auch einen Punkt (-4| 7).
Und schon hast du zwei Zeilen in deinem LGS.
Aber aufpassen: nur x durch -x ersetzen. Die y-Werte sind identisch.
Hat dieser Punkt eine Eigenschaft, z.B. Tiefpunkt zu sein, dann gilt das auch für seinen Kontrapunkt.
Das erhöht die Anzahl der Gleichungen jeweils um 1. Und das ist ja auch ganz gut so, wenn man nach Zeilen für das LGS fahndet.
symmetrie wurde ja schon erklärt. hier noch ein bild dazu.
dann:
achsensymmetrisch ist die funktion 4.grades nur falls kein glied mit x3 oder x vorkommt.
f ( x ) = a*x4 + b*x2 + c
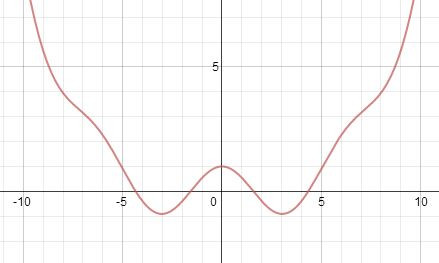
Was sich links und rechts der y-Achse befindet, ist deckungsgleich.
Wenn du das Papier genau auf der y-Achse falten würdest, fallen beide Kurventeile direkt aufeinander.
das heißt dass wenn man den graph genau an der y achse falten würde, diw graphen genau übereinander wäre. also die achse ist die symmentrieachse des graphen
Die Bedingungen, die sich daraus ergibt ist:
f(x) = f(-x)
und
f'(x) = -f'(-x)