Warum ergeben alle Zahlen, die man hoch null nimmt immer 1?

Diese Frage habe ich schon 2 mal beantwortet... nun zum 3.:

http://www.gutefrage.net/frage/warum-ist-a-hoch-0-gleich-1

und

http://www.gutefrage.net/frage/wieso-ist-eine-zahl-hoch-0-immer-1

Wenn man die universelle Formel statt der Spezialfall-Formel (ganzzahlige x mal mit sich selbst multiplizieren) nimmt, wird alles klar:

Dabei bedeutet Potenzieren mit reellen Zahlen:

a^x = e^(log(a)*x)

bei x=0 bedeutet das innere der Klammer: Produkt mit 0 bleibt 0

(außer Polstellen wie + oder - UNENDLICH)

Über bleibt also e^0 = exp(0)

Exponentialfunktion kann z.B. per Reihenentwicklung beliebig genau berechnet werden:

e^x = 1 + x/1! +x²/2!+... 

 bei x=0 bleibt 1 über (Rest wird durch Ausklammern zu 0) -> fertig.

Die Bilder dazu in den beiden anderen LINKs...

Das ist eine Folge der definierten Potenzen und ihrer Regeln, denn
a⁰
ist ja nichts im eigentlichen Sinn Reales, sondern auch eine Definition, - allerdings wohldefiniert, wie man sagt.

aⁿ / aⁿ = 1           Da besteht kein Zweifel. Das weiß man schon aus dem 1x1.
Nach dem 2. Potenzgesetz gilt:

aⁿ / aⁿ  =  aⁿ⁻ⁿ  =  a⁰

Wir haben gerade gesehen, dass derselbe Quotient gleich 1 ist, daher

a⁰ = 1

Da gibt es mehrere  mögliche Erklärungen für (im Folgenden gilt x ≠ 0).

Am besten und anschaulichsten geht das mit einer Analogie:

x³ = x * x * x = x² * x
x² = x * x = x¹ * x
bzw. allgemein xⁿ = xⁿ⁻¹ * x

Daraus folgt: x¹ = x⁰ * x = x

Somit muss gelten, dass x⁰ = 1

Oder auch so:

x² = x³/x
x¹ = x²/x
bzw. allgemein xⁿ = xⁿ⁺¹/x

Daraus folgt: x⁰ = x¹/x = x/x = 1

Im Übrigen: Die Begründung isso gilt nicht. ^^

LG Williebrgi

Ich finde es auch immer recht anschaulich, wenn man sich mal diese Aufstellung ansieht (die 3 ist nur ein Beispiel für eine Basis, auch mit anderen Zahlen siehst Du, dass die Ergebnisse der Potenzen, wenn diese gegen 0 gehen, immer näher an die 1 heranrücken und erst bei negativen Potenzen darunter):

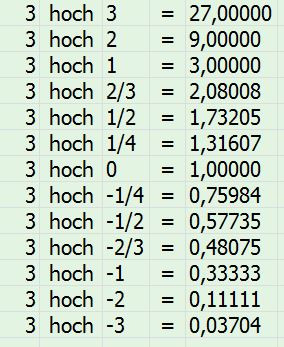
Weil die Zahl selber nicht vorhanden ist (nämlich 0-mal) und die 1 das neutrale Element der Multiplikation ist. Hoch-irgendwas basiert ja auf mehrmaliger Multiplikation.

Letztendlich ist es Definitionssache, aber das als 1 zu definieren macht am meisten Sinn.