Verständnisproblem Statik, schräger Balken?
Hey Leute, ich habe ein kleines Verständnis Problem in der Statik.
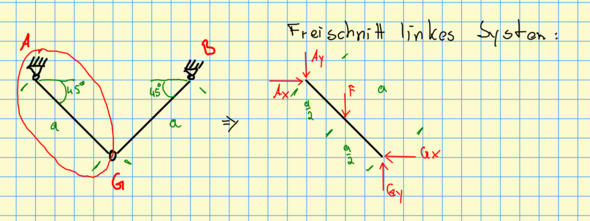
In dem Bild findet Ihr ein statisches System mit zwei schrägen homogenen Balken, zwei Festlagern und einem Gelenk.
Die Balken sind durch ihre Gewichtskraft F belasetet, welche ja im jeweiligen Schwerpunkt bei a/2 senkrecht angreifen.
Ich habe das linke System mal freigeschnitten und die Lager durch die Lagerreaktionen ersetzt. Nun möchte ich die Lagerkräfte bestimmen und frage mich, ob Ax und Gx überhaupt Kräfte aufnehmen, denn der Balken überträgt die senkrechtwirkende Gewichtskraft doch auch nur in die senkrechtwirkende Y-Richtung, sodass Lager A und G in X-Rcihtung, also Ax und Gx keine Kräfte aufnehmen, oder?
Ich bin mir da nämlich nicht so sicher :/
2 Antworten
Hier ist Ay=-F Ax=-F/2 Gy=0 Gx=-Ax
Warum ?
Wegen der Symmetrie des Systems (auch in der Belastung) wird ja in G keine Vertilalkraft übertragen.
Gx leistet allein die Gegendrehung um A aus F*2 (jedes Kästchen deiner Skizze =1).
Also F*2+Gx*4=0
Hey, ersteinmal vielen Dank für deine Antwort! :)
Eigentlich geht es in dieser Aufgabe um das maximale Biegemoment. Ich weiß, dass das bei a/2, aber ich bekomme immer genau den doppelten Wert raus, als das Ergebnis in der Musterlösung (Musterlösung ohne Rechneweg).
Und ich glaube, dass meine Fehler bei den Lagerkräften liegt, denn ich habe Gx = Ax raus und nicht wie du Gx = -Ax.
Ich finde den Fehler einfach nicht und bin schon am verzweifeln. Ich hänge schon echt lange an der Aufgabe, obwohl ich die garnicht soo schwer finde, aber irgendwo hat sich der Fehlerteufel eingeschlichen, auf den ich einfach nicht komme.
Findest du ihn? :) Ich lade nochmal ein Bild meiner Rechnung in den Antworten hoch.
Natürlich gibt es auch horizontal wirkende Kräfte !
1.) Da der Stab selber nur Kräfte in seiner Längsrichtung aufnehmen kann, muss (wegen dem 45°-Winkel) gelten: |Ax| = |Ay| sowie |Gx| = |Gy|
2.) Kräftesumme horizontal gleich Null: |Ax| = |Gx|
3.) Kräftesumme vertiktal gleich Null: Ay + F +Gy = 0 (vektoriell ! Richtungen beachten)
Da der Stab selber nur Kräfte in seiner
Längsrichtung aufnehmen kann,
Diese Aussage ist wohl ziemlich daneben.
Hier ist z.Bsp. Ay=-F und Ax=-F/2.