Trigonometrie Astronomische Entfernungen?
b) Aristarch von Samos stellte folgende Überlegung an, um die Entfernung Erde-Sonne mit der Entfernung Erde-Mond vergleichen zu können. Bei Halbmond bilden Erde, Mond und Sonne ein rechtwinkeliges Dreieck. Aristarch schätzte den Winkel epsylon auf mindestens 87"
Gib aufgrund von Aristarchs Schätzung für epsylon an, wievielmal weiter die Erde von der Sonne als vom Mond entfernt ist!
Tatsächlich ist die Erde etwa 400-mal weiter von der Sonne als vom Mond entfernt. Gib einen korrekteren Wert für epsylon an!

Kann mir wer helfen? Nicht vorrechnen, sondern Vorgang erklären, bitte!
Danke :)
2 Antworten
Benutze die Trigonometrischen Gleichungen, um aus dem Winkel das Verhältnis zwischen den Seiten zu berechnen.
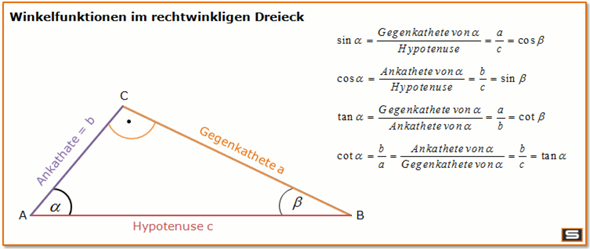
In diesem Bild wäre Alpha der Winkel Epsilon, b die Distanz Erde-Mond und c die Distanz Erde-Sonne
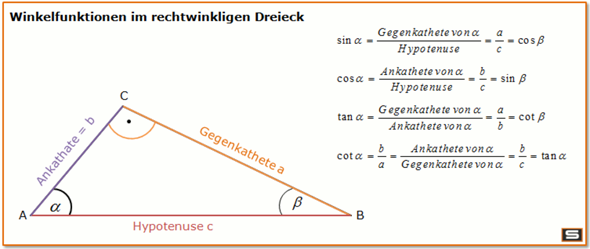
Nur eine Bemerkung:
Die Idee Aristarchs, diese Frage mittels einfacher Trigonometrie zu beantworten, in allen Ehren. Trotzdem ist diese Methode für die praktische Durchführung ziemlich unpraktisch, aus verschiedenen Gründen, von welchen ich nur ein paar anführen möchte:
(1.) Die Bestimmung des exakten Zeitpunktes von "Halbmond" ist schwierig und mit den damaligen Mitteln (ohne Uhren) praktisch nicht wirklich machbar.
(2.) Die Messung eines solchen Beobachtungswinkels ist ebenfalls nicht ganz leicht durchführbar, wenigstens ohne modernes Instrumentarium.
(3.) In vielen Situationen, wo Sonne und Halbmond gleichzeitig sichtbar sind, steht mindestens einer dieser Himmelskörper nur knapp über dem Horizont. Deshalb muss man dann auch noch mit "Verfälschungen" des zu messenden Winkels durch die Lichtbrechung in der irdischen Atmosphäre rechnen.