Thema Preis-Absatz-Funktion in Mathe/Kaufmännisches Rechnen?
Hallo miteinander, schreibe nach den Ferien eine Klausur über dieses Thema. War die letzten Mathe Stunden leider nicht in der Schule und verstehe dieses Thema nicht. Kann mir jemand bei dieser Aufgabe behilflich sein? Habe schon etliche Lösungswege ausprobiert, auch durch YT Videos doch hat mir bisher noch nichts weitergeholfen.. Danke im Voraus! Die Preis-Absatz-Funktion eines Monopolisten lautet: pN (x) = -0,5x+30. Er produziert sein Gut entsprechend der Kostenfunktion K(x) = 12x + 15.
a.) Ermitteln Sie den ökonomischen Definitionsbereich. b.) Bestimmen Sie den Höchstpreis und die Sättigungsmenge c.) Berechnen Sie die Gleichungen der Erlösfunktion und der Gewinnfunktion. d.) Bestimmen Sie die Produktionsmengen, für die der Monopolist sein Gut mit Gewinn anbieten kann. Geben Sie auch die entsprechenden Preise an. e.) Bestimmen Sie das Erlösmaximum und das Gewinnmaximum.
1 Antwort
Da das ja eine Menge Fragen sind, begnüge ich mich mal erst mit ein paar Andeutungen. Falls Du dann weitere Fragen hast, heraus damit.
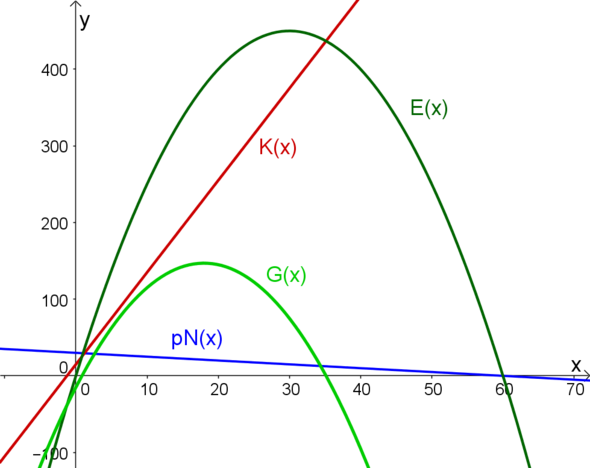
Wichtig vorweg: Es geht hier immer um alles, was mit Produktion und Verkauf zu tun hat. Dabei gibt x grundsätzlich eine Produktion(=Verkaufs)menge an. Mit den Funktionen p, E, K und G bestimmst Du jeweils den Preis, den Erlös, die Kosten und den Gewinn, den Du bei einer bestimmten Menge x hast.
Ich habe ein Bild zu den Funktionen erstellt, meine Erfahrungen mit dem Hochladen sind aber nicht gut. Falls Du kein Bild siehst, wende Dich mal an GF (habe ich auch schon gemacht).
a) Deine Funktionen machen mathematisch für jedes beliebige x einen Sinn, nicht jedoch ökonomisch. So kannst Du keine negativen Mengen produzieren. Auch negative Preise gibt es nicht. Also ist die Definitionsmenge begrenzt durch x = 0 sowie die Nullstelle von pN.
b) Hat sehr viel mit a) zu tun...
c) Wie berechnest Du den Erlös? Indem Du die verkaufte Menge mit dem Preis malnimmst. Gewinn dürfte eigentlich klar sein: vom Erlös die Kosten abziehen.
d) Hier sind die Nullstellen gefragt. Welche Form hat die zu G gehörende Parabel? Für welche x verläuft die Parabel oberhalb der x-Achse (also mit positiven y-Werten)?
e) E und G sind beides quadratische Funktionen, die zugehörigen Parabeln nach unten geöffnet. Also liegt der jeweilige Scheitelpunkt bei beiden oben. Von beiden ist der y-Wert gesucht. Stichworte: Scheitelpunktform - quadratische Ergänzung.
So, nun hast Du erst mal zu tun :-)
bei der d. bin ich auch noch ein bisschen überfragt. Habe für die Nullstellen x1 = 35,15 und x2 = 0,85 raus. Habe das dann in meine Funktion eingesetzt (um die entsprechenden Preise auszurechnen, ist der Schritt richtig!?) und bei 0,85 kam -5,28 raus!? Das ergibt doch keinen sinn.
Die Preisfunktion ist ja eine lineare Funktion mit negativer Steigung (fallende Gerade). Das bedeutet: Je mehr Du produzierst, desto geringer wird der Preis am Markt (hat ja was Logisches).
Somit ist der höchste Preis bei der geringsten Menge (x=0). Umgekehrt: Will keiner mehr was für die Ware zahlen (p=0), ist der Markt gesättigt (Nullstelle von p berechnen).
Vielen dank für die Antwort! Aber was meinst du damit, dass die b. Sehr viel mit der a zu tun hat? Das hilft mir gerade nicht weiter..