Relation | Äquivalenzrelation oder Halbordnung?
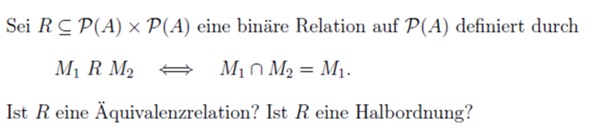
Ich verzweifle förmlich an dieser Aufgabe! Ich kann nur begründen, dass es nicht symmetrisch sein kann (somit ist Äquivalenzrelation ausgeschlossen). WIe begründet man den Rest??? (Reflexivität, Antisymmetrie und Transitivität)
Wichtig noch zu wissen: M_1 ist eine Teilmenge von M_2 ist eine Teilmenge von A und M_1 vereinigt M_2 = M_2
1 Antwort
Woran genau scheitert es denn? Für Reflexivität z.B. musst du ja prüfen, ob für alle M in P(A) gilt, dass M R M ist, also dass M ∩ M = M gilt. Das ist eine Mengengleichheit, die du entweder allgemein beweisen oder durch ein Gegenbeispiel widerlegen kannst.
Bei Antisymmetrie und Transitivität musst du ebenfalls "nur" die Definitionen checken. Wenn du jeweils deinen bisherigen Stand / Ansatz zeigst, könnte ich drüber gucken und wir sehen weiter.
Das mit der 1h wird sportlich ;)
M1 und M2 sind keine festen Mengen der Aufgabenstellung. Die Definition der Relation lautet einfach: Für Mengen M1, M2 in P(A) ist M1 R M2 genau dann, wenn
M1 ∩ M2 = M1
gilt. Hier sind M1 und M2 also einfach nur "Variablen".
Und für Reflexivität muss man sich nun fragen: Gilt M1 R M1 für alle Mengen M1 in P(A)? Aber da der Name meiner Variablen egal ist und ich in dieser Aussage nur eine Menge habe, hab ich M1 eben in M umbenannt.
Bei der Aufgabe davor waren die halt feste Mengen, das hier ist Aufgabe (b). Darum hab ich bei der Ergänzung noch was hingeschrieben. Aber glaube trz du hast recht
Neue Aufgabe, neue Definitionen (oder so). Die Aufgabe ergibt keinen Sinn, wenn M1 und M2 fest sind.
Also meine Begründung dafür, dass es nicht symmetrisch sein konnte war, dass M_1 eine Teilmenge von M_2 ist und beide nicht gleich sind, womit nicht alle Elemente in Beziehung stehen können. Wäre das dementsprechend jz falsch?
Ja, das ist ja keine Voraussetzung mehr.
Darf ich fragen, was du in Aufgabe (a) bewiesen hast? Eventuell lässt sich das für (b) verwenden.
Zeigen Sie, dass für zwei Teilmengen M1 ⊆ A und M2 ⊆ A von A gilt:
M1 ∩ M2 = M1 ⇐⇒ M1 ∪ M2 = M2 ⇐⇒ M1 ⊆ M2.
Hab das bewiesen
Ah, ok. Das heißt, du weißt bereits, dass in (b) gilt:
M1 R M2 ⇐⇒ M1 ⊆ M2.
Das macht quasi alles deutlich einfacher ;) Probiers nochmal damit.
Konnte ja damit nur aussagen, dass es halt nicht symmetrisch sein kann. Wie soll ich damit die anderen Eigenschaften zeigen? ;-----;
Tut mir auch leid, falls ich deine Zeit grad sehr beanspruche. Schonmal danke, dass du mir überhaupt hilfst. Das ist ja sowieso nicht selbstverständlich
Du musst halt die Definition nachrechnen:
- Ist M ⊆ A, so gilt M R M [Reflexivität]
- Ist M1 R M2 und M2 R M1, so gilt M1 = M2 [Antisymmetrie]
- Ist M1 R M2 und M2 R M3, so gilt M1 R M3 [Transitivität]
Und durch ein Beispiel widerlegen:
- Ist M1 R M2, so gilt M2 R M1 [Symmetrie].
Wenn du jetzt überall das R durch ⊆ ersetzt (was du ja darfst, weil M1 R M2 äquivalent zu M1 ⊆ M2 ist), sind das Aussagen, die du entweder schon kennst oder wirklich leicht zu beweisen/widerlegen sind.
Aber dann kann ja auch Antisymmetrie nicht gelten, weil M_1 ungleich M_2?
Nirgendwo in der Aufgabe steht, dass M1 und M2 verschiedene Mengen sein müssen.
Nja, grundsätzlich hab ich halt die Vorstellung wegen (a), dass M_1 in M_2 ist und M_2 in A, weil sie auch in der Reihenfolge Teilmengen voneinander sind. Aber vielleicht denke ich zu sehr nach zwischen den Zusammenhängen der Aufgaben
Auch in (a) steht nirgends, dass M_1 und M_2 verschieden sein müssen. M_1⊆M_2 bedeutet ja nicht automatisch, dass die Mengen verschieden sind.
Aber in (a) stand doch die Schnittmenge zwischen M_1 und M_2 =M_1 und die Vereinigungsmenge von M_1 und M_2 ergibt M_2. Also muss M_1 in M_2 liegen und hat halt weniger Elemente
und hat halt weniger Elemente
Und eben das ist einfach falsch. Wenn M_1 = M_2 ist, wäre jede dieser Aussagen immer noch korrekt.
Aber dann ist doch meine Begründung für die Nicht-Symmetrie doch falsch
Stimmt, wie gesagt solltest du dafür ein Gegenbeispiel finden ;)
OMG DU BIST EIN GENIUS. GLAUBE ICH HABE ES JETZT VERSTANDEN
Ey rly nochmal vielen Dank, dass du mir geholfen hast. Konnte das alles abarbeiten in der kurzen Zeit. Vielleicht nicht ganz sauber, aber zumindest hab ich es. Kuss geht raus <3
Sry btw, falls ich so verzweifelt wirke, aber ich sitze schon eine ganze Weile an dieser Aufgabe
Ich hab eher eine Frage: Wieso schreibst du für Reflexivität M R M? Ist nicht eher M_1 R M_1 und M_2 R M_2 richtig? Und ich verstehe halt nicht, wie ich Antisymmetrie und Transitivität auf diesem Bsp. anwenden soll, iwie fühle ich mich überfordert. Darum finde ich für beide keinen wirklichen Weg das ordentlich zu begründen. Es wäre rly gut, wenn du mir zeigen könntest, wie man das angehen soll... Muss halt die Aufgabe auch in ca. 1h abgeben :/