Regelmäßige Sechseckpyramide, wie bekomme ich a?
Hallo! Und zwar habe ich eine Aufgabe bei der nur
h=24cm
und
ha=7cm
gegeben ist.
hs konnte ich schon hs ausrechnen, jetzt weiß ich allerdings nicht wie ich a Berechnen kann.
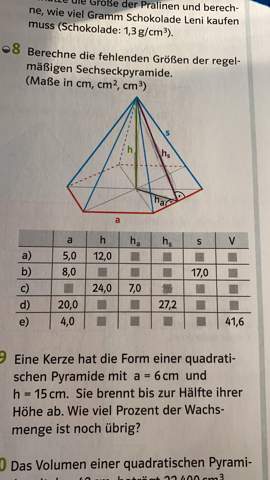
4 Antworten
Wie wir ja alle wissen gilt für Die Höhe h von a, in einer sechseckigigen Pyramide, welche gleichseitig ist:
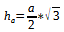
Wir müssen also nur nach der Seitenlänge a umstellen und dann einsetzen:
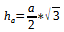
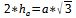
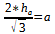
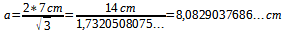
Und so können wir aus der Höhe von a die Seitenlänge a herrausfinden.^^
Bei Fargen hierzu können Sie sich immer gerne an mich wenden.
Ich hoffe, dass ich Ihnen damit weiterhelfen konnte.
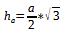
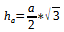
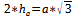
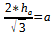
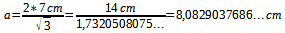
a= Wurzel aus 4:3 ( 1.54700 .. ) mal ha ( 7 cm ) = 8.08 cm. Auf der Grundfläche hast du 6 gleichseitige Dreiecke mit 3 x a. Es gilt a hoch2 + b hoch2 =c hoch 2. Eine Seite sei eins, dann teilt ha die Seite a in 2 Hälften. In dem einen Teildreieck gilt also ha = 1hoch2 - 1/2 hoch2 = ha hoch2. ha ist also die Wurzel aus 0.75. Die Seite a ist 1: Wurzel 0.75 so gross wie ha, also 8.08 cm
Wenn du ha hast, kannst du mit Pythagoras auch a ausrechnen, denn alle diese Grunddreiecke sind gleichseitige Dreiecke.
Also eine Gleichung mit einer Unbekannten (a).
ha^2 + (a/2)^2 = a^2
a ~ 8,08 cm
Danke! Aber wie ist der Weg? a fehlt ja, was soll ich einsetzen oder wie soll ich umstellen? Tut mir leid, dass ich nochmal Fragen. Ich steh aufm Schlauch😅.
Die Grundfläche besteht aus 6 gleichseitigen Dreiecken mit der Seitenlänge a
Aus ha berechnest Du a mit dem Pythagoras:
(ha)² + (a/2)² = a² >> ha = 2 • a / √3
Vielen Dank! Sie haben mich gerettet😊🙈.^^