Raum-Zeit Krümmung vorstellen, wie?
Guten Tag,
ich versuche mir die Raum-Zeit Krümmung und die Gravitation eines Objektes (z.B. Sonne oder schwarzes Loch) im 3D Universum Bildlich vorzustellen. 2D kriege ich hin, bei 3D kommt mein Gehirn aber irgendwie nicht mit.
Kann mir jemand helfen mir die Raum-Zeit Krümmung in einem 3 Dimensionalen Raum besser zu veranschaulichen? Vielen Dank!
4 Antworten
Hallo DebugMyMind,
in „Full Scale“ gar nicht, so anschaulich - was übrigens nicht nur an der Anzahl der Dimensionen liegt. Übrigens sind auch höherdimensionale Räume, wenngleich nicht anschaulich, so doch mathematisch zugänglich. Um das zu „übersetzen“, können Hilfsvorstellungen nützlich sein, sind aber mit Vorsicht zu genießen. Wie Folgendes.
1 Das Bild mit dem Gummituch......eignet sich besser zur Veranschaulichung von Potentialdifferenzen (auch elektrischen) als zur Veranschaulichung der Krümmung der Raumzeit. Eine Murmel nämlich würde der Gravitation der Erde unter dem Gummituch folgen, nicht etwa der Krümmung des Tuches.
So würde sie auch nach außen rollen, wenn das Tuch nach oben gewölbt wäre. Eine Roboter-Ameise hingegen, die auf’s Geradeausgehen programmiert wäre, würde in beiden Fällen der Krümmung folgen und je nach Pfad tatsächlich nach innen abgelenkt.
2 Innere KrümmungMit Krümmung ist übrigens keineswegs eine Krümmung in eine zusätzliche Dimension gemeint, sondern - wie @noskill schreibt - die Krümmung einer Mannigfaltigkeit (das ist die Verallgemeinerung einer Fläche in mehreren Dimensionen) in sich, die sich, wie GAUß herausfand, ohne Bezug auf Einbettung in einen höherdimensionalen Raum beschreiben lässt.
Die augenscheinlich krumme Fläche eines Zylinders beispielsweise ist überhaupt nicht gekrümmt; ein zusammengerolltes Blatt Papier lässt sich auf einem ebenen Tisch ausrollen, ohne es zu verzerren. Das wäre weder mit der Oberfläche eines Balls (positive Gauß’sche Krümmung (k>0); der würde sich dehnen oder reißen) noch mit einer Tuba-förmigen Fläche möglich (negative Gauß’sche Krümmung (k<0), die würde Falten werfen).
Die Gauß’sche Krümmung einer Fläche ist die Abweichung von der sog. Euklidischen Metrik
(1.1) Δs = √{Δx² + Δy²},
die mit wachsender Skala immer größer werden, während für zwei eng benachbarte Punkte im 3D-Raum
(1.2) ds² = √{dx² + dy² + dz²}
noch immer gilt. Im ganz Kleinen ist auch die Winkelsumme im Dreieck ziemlich genau 180° und das Verhältnis zwischen Umfang und Durchmesser eines Kreises etwa π; auf größeren Skalen wachsen die Abweichungen. Vor allem gilt für geodätische Linien, die Verallgemeinerungen von Geraden, nicht Euklids Parallelenaxiom. Vielmehr gibt es Fälle, in denen stellenweise parallel verlaufende Geodätische immer irgendwo zusammenlaufen (z.B. Großkreise auf einer Kugeloberfläche) oder auseinanderlaufen (Sattelfläche).
Allerdings ist Gravitation ja Krümmung der Raumzeit, nicht des Raumes.
3 Die Lichtgeschwindigkeit und die Metrik der RaumzeitDie Raumzeit ist erst einmal einfach die Zusammenfassung von Zeit und Raum, wobei sehr wohl zwischen einer räumlichen Weglänge ds und einer zeitlichen Weglänge dτ zu unterscheiden ist.
Genauer festgelegt wird der Zusammenhang zwischen dτ und einer Koordinaten-Zeitspanne dt dadurch, dass MAXWELLS Elektrodynamik unabhängig vom Bezugssystem bzw. Bezugspunkt O sein muss. Deren Grundgleichungen enthalten die Lichtgeschwindigkeit c. Das bedeutet aber auch, dass sich Licht relativ zu O und relativ zu einem seinerseits relativ zu O mit v› bewegten Punkt O’ mit c ausbreiten muss:
(2.1) dτ² = dt² – ds²/c² ≡ dt’² – ds’²/c²
Diese Abstandsdefinition nennt man eine Pseudo-Euklidische oder MINKOWSKI-Metrik, benannt nach einem Lehrer von EINSTEIN.

Das Minuszeichen in (2.1) sorgt dafür, dass die rechte Seite 0 ist, wenn es die linke ist (Ereignisse wie die Emission und Absorption eines und desselben Lichtsignals) und dafür, dass der Unterschied zwischen Zeit und Raum bestehen bleibt; unter raumartig getrennten Ereignissen versteht man solche, für die ds > cdt ist; dann ist (2.1) negativ und dafür
(2.2) dς² = ds² – c²dt² ≡ ds’² – c²dt’²
positiv; die Quadratwurzel daraus ist natürlich der Abstand in dem Koordinatensystem, in dem beide Ereignisse gleichzeitig sind. Die zeitliche Reihenfolge raumartig getrennter Ereignisse hängt nämlich vom Bezugssystem ab (das ist übrigens ein Grund, warum Überlichtgeschwindigkeit nicht möglich ist; anderenfalls könnte man „über Bande“ in die Vergangenheit gelangen).
Krümmung der Raumzeit sind also Abweichungen von der MINKOWSKI - Geometrie.
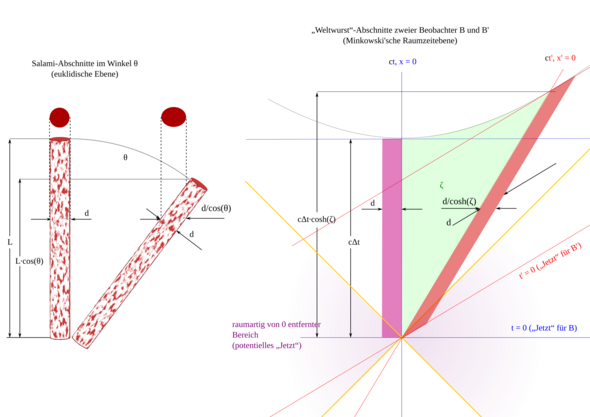
4 Ob Du in der Raumzeit einer Geodätischen folgst, spürst DuEin Körper, dessen Weltlinie (angebrachter wäre bei einem ausgedehnten Körper vielleicht „Weltstrang“ oder „Weltwurst“) eine Geodätische ist, ,,spürt” keine Trägheitskräfte (und auch keine Schwerkraft).
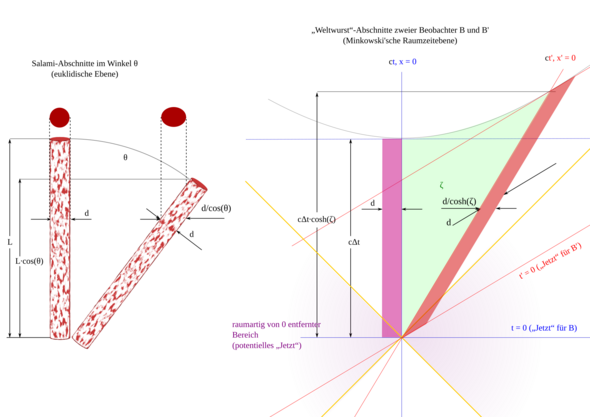
Ein Koordinatensystem dieser Art heißt ein Inertialsystem. Die Anwesenheit eines homogenen Schwerefeldes macht hier keinen Unterschied, man kann es wegtransformieren.
Einsteins Allgemeine Relativitätstheorie (ART) beruht nämlich darauf, dass sich rein physikalisch homogene Schwerefelder von der Wirkung einer linearen Beschleunigung (Trägheitskraft) nicht unterscheiden lassen; das ist Einsteins Äquivalenzprinzip.
In der Realität, mit Gravitationsfeldern, die nicht homogen sein müssen, gibt es Inertialsysteme nur lokal/temporal. Manche geodätischen Linien enden abrupt, etwa die eines Beobachters, der nach freiem Fall auf die Oberfläche eines Planeten aufprallt. Außerdem sind Gravitationsfelder von realen Himmelskörpern inhomogen, sodass Gezeitenkräfte auftreten können, die sich nicht wegtransformieren lassen.
Und natürlich nähern sich im Weltraum Körper einander, was auf eine positive Gauß’sche Krümmung (bzw. deren Entsprechung) hindeutet: ursprünglich parallele Weltlinien laufen zusammen.
Raumkrümmung zeigt sich übrigens erst spür- oder sichtbar, wenn die Gravitationsfelder erheblich sind. Die Sonne beispielsweise schafft es immerhin, einen - bei einer totalen Sonnenfinsternis sichtbaren uns insbesondere messbaren - Gravitationslinseneffekt zu erzeugen.
3 Eine Bemerkung zur RelativitätstheorieDie Relativitätstheorie sollte eigentlich einfach Klassische Physik heißen.
Das, was wir unter diesem Namen kennen, sollte künftig Klassische Physik genannt werden, weil sie eine Näherung für spezifische potentielle bzw. kinetische Energien ist, deren Beträge klein im Vergleich zu c² sind und der Unterschied zwischen τ und t bzw. t’ vernachlässigt werden kann.
Das sind die tatsächlichen Verhältnisse, nicht etwa so, wie es aus historischen Gründen immer noch gelehrt wird: Der Newton-Limes als die (normale) Klassische Physik und unter ,ferner liefen’, für die ganz Abgedrehten bzw für ganz abgefahrene Spezialfälle eine Extra-Theorie. Nein, ,Newton’ ist der Spezialfall, ,Einstein ‘05’ (SRT) ein allgemeinerer und ,Einstein ‘15’ (ART) ein noch allgemeinerer Fall.

Das ist auch nichts was man sich auch vorstellen kann da wir zeit nicht visualisieren können. Es ist quasi die 4. Dimension.
Es gibt zwar bilder im netz aber die sind mehr oder minder nur um irgendeine vorstellung davon zu haben.
Das tuch ist aber 3 Dimensional qenn man das über eine kugel zb legt.
Du hast eine tiefe, breite ubd Höhe.
Ausser das die krümmung nicht einseitig sondern Rundherum ist ( bei einer kugel)
Das tuch ist aufgrund der Gravitation einseitig gekrümmt.
Ach stimmt, ich bin doch doof. Ich habe die Tiefe des Tuches außer acht gelassen. Du hast Recht.
Wie kann ich mir eine Krümmung rundherum um eine Kugel vorstellen? Da hapert es jetzt noch...
Spiegel einfach das Bild. Vorallem das vorher und nachher.
Ja es hapert natürlich^^ wie gesagt nicht wirklich vorstellbar
Kann ich mir beim Vorstellen die Zeit wegdenken?
Das wäre kontraproduktiv. Gekrümmt ist nämlich die Raumzeit, und zwar schon „lange bevor“ der 3D-Raum gekrümmt ist.
In 2 Raumdimensionen hätte man ja z.B. ein Tuch auf das man ein schweres Objekt legt und dies spannt dann das Tuch nach "unten".
Das Bild taugt ganz gut dazu, Potentialdifferenzen (auch elektrische) zu veranschaulichen, ist aber irreführend, wenn es um die Krümmung der Raumzeit geht.
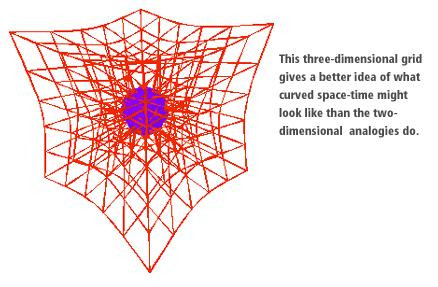
Es handelt sich um ein Gitternetz aus Würfeln, die durch die Krümmung der Raumzeit "verzogen" werden. - Eine bessere Darstellung im 3-dimensionalen Raum ist mir nicht geläufig.
Im Prinzip kann man sagen, dass sich das "Koordinatensystem" staucht/dehnt.
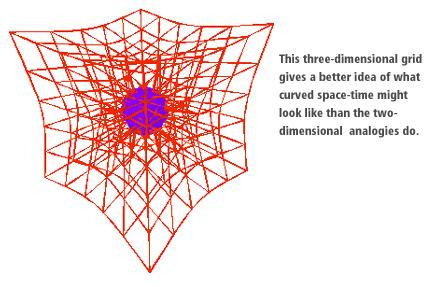
ja endlich mal ein bild welches die krümmung nicht auf einer ebene darstellt...diese ist wesentlich logischer und verzerrt nicht die tatsachen !
Wohl kaum.
Kann ich mir beim Vorstellen die Zeit wegdenken? Also sodass ich nur 3 Raumdimensionen habe?
In 2 Raumdimensionen hätte man ja z.B. ein Tuch auf das man ein schweres Objekt legt und dies spannt dann das Tuch nach "unten". Wie wäre es bei einem 3 Dimensionalen Raum, ohne Zeit?