Quadratische Gleichung berechnen?
Wie rechnet man diese Aufgabe?

2 Antworten
Hey 😁
Hmm das schreit nach einer Umformung zur Normalform und dann musst du natürlich die PQ-Formel verwenden. Das ganze machst du um gegebenenfalls die Schnittstellen mit der X-Achse (Nullstellen) herauszufinden. Das ist ganz einfach. Ich zeig dir mal, wie das geht 😇:
gegeben: 3.5 x^2 - 8.75x + 3.5 = 0
1. Schritt: Bringe die quadratische Gleichung in eine Normalform [x^2 + ax + b = 0] 👈🏻
3.5 x^2 - 8.75x + 3.5 = 0 | :3.5
x^2 - 2.5x + 1 = 0 => Normalform 🙌🏻*
2. Nun nutzen wir die PQ-Formel. Unser P ist -2.5 und unser Q ist 1 👈🏻
(Die '1/2' nach dem X soll tiefgestellt sein. Kann das leider hier nicht darstellen. Beim '+-' steht das plus oben und minus unten, wie bei einem Bruch ohne Bruchstrich 😉)
x1/2 = (- p/2) +- die Wurzel aus ((p/2)^2 - q)
x1/2 = - (-2.5/2) +- die Wurzel aus ((p/2)^2 - q)
x1/2 = 1.25 +- die Wurzel aus ((-2.5/2)^2 - 1)
x1/2 = 1.25 +- die Wurzel aus ((-2.5/2)^2 - 1)
x1/2 = 1.25 +- die Wurzel aus ((1.5625 - 1))
x1/2 = 1.25 +- die Wurzel aus (0.5625)
x1/2 = 1.25 +- 0.7
x1 = 1.25 - 0.7 = 0.55
x2 = 1.25 + 0.7 = 2
3. Schritt: Viele vergessen ihn, aber er ist essentiell. Schnittpunkte aufschreiben (wenn vom Lehrer 👨🏻🏫 verlangt) 👈🏻
N1(0.55 | y1)
N2(2 | y2)
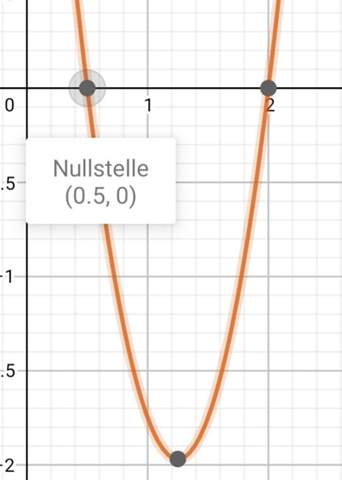
Hey aber da fehlen uns noch 2 Y-Werte ☹. Was hat das zu bedeuten und wie kriegen wir diese heraus? Vielleicht hilft uns ein Blick in den Graphen..🧐
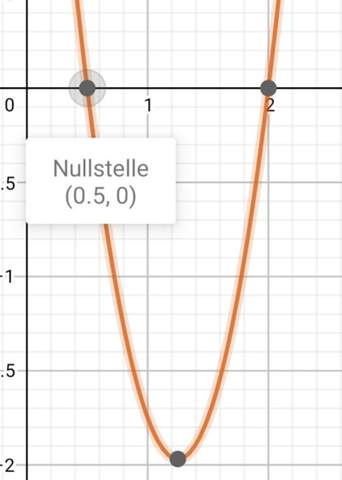
Ahh 😆 stimmt wir haben Nullstellen berechnet. Also ist der Y-Wert bei beiden y = 0. Die Punkte liegen ja auf der x-Achse. Somit lauten die Nullstellen:
=> N1(0.55 | 0)
=> N2(2 | 0)
Generell würde ich dir raten, wenn du Schwierigkeiten hast nach Online Rechnern wie GeoGebra zu schauen, damit du das Ergebnis nachvollziehen kann. Denn aus Fehlern lernt man und verringert die Wahrscheinlichkeit das man sie erneut macht 🤓
Hoffe ich konnte dir helfen,
Grüße Irene 😇
Hallo,
dann dividiere doch erst einmal durch 3,5.
Dann musst du die pq-Formel anwenden.
x²-2,5x+1=0
x=1,25±√(1,5625-1)
x=1,25±0,75
oder mit quadratischer Ergänzung:
x²-2,5x+1=0
x²-2•x•1,25+1,25² - 1,25²+1=0
(x-1,25)² -1,5625+1=0
(x-1,25)²=0,5625
x-1,25=±0,75
x=1,25±0,75
x=0,5 oder x=2
🤓
Die pq-Formel habe ich noch nicht gehabt.