Python Baum programmieren?
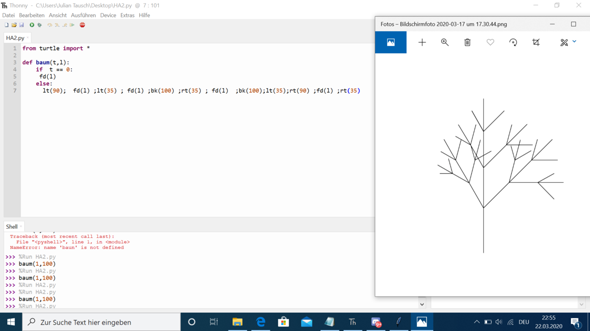
Ich brauche hilfe, ich weiß nicht wie ich das programmieren soll. Ich will wissen wie ich das Programmieren kann, ich brauche auch keine Lösung. (Ich muss den Baum im rechten Fenster programmieren)
3 Antworten
Konzentriere dich erst einmal auf die Grundstruktur des Baums. Es gibt einen Knoten und der teilt sich in regelmäßigen Abständen in drei Äste. Linker und rechter Ast sollten in einem bestimmten Winkel relativ vom Stammast abstehen.
Dies zu zeichnen - nichts weiter - sollte dein erster Startpunkt sein.
Der nächste Schritt, wenn du das hast, wäre es, dir dafür eine Funktion zu schreiben. Diese Funktion bekommt einen Startknoten überreicht und zeichnet dazu dann die Äste. An dieser Stelle kann aber auch gleich die nächste Bedingung beachtet werden:
Umso höher er geht, umso mehr flacht die Tiefe des Astwerks ab (die erste Verzweigung hat drei Unterteilungen, die zweite Verzweigung hat zwei Unterteilungen, die dritte Verzweigung hat nur eine Unterteilung).
Und da kommt auch schon die Rekursion ins Spiel. Ausgehend vom ersten Ast sollte sich die Funktion immer wieder selbst aufrufen. Damit sie die obige Bedingung erfüllt und irgendwann auch abbricht, könnte ein Parameter dienlich sein, der angibt, wie oft sich die Verzweigung noch wiederholen soll.
So dürfte der Algorithmus aussehen:
verzweige(startpunkt, n)
wiederhole n-Mal
zeichne linken Ast und merke Endpunkt der Linie
verzweige(linker Endpunkt, n - 1)
zeichne mittleren Ast und setze Endpunkt als neuen Startpunkt
zeichne rechten Ast und merke Endpunkt der Linie
verzweige(rechter Endpunkt, n - 1)
Gezeichnet wird immer ausgehend vom Startpunkt. Den Stamm am Anfang, bis zur ersten Verzweigung, müsstest du vor Aufruf der Methode noch extra zeichnen.
Zeichne den Algorithmus am besten einmal mit Paint nach, um ihn besser zu verstehen. Immer wenn verzweige aufgerufen wird, ruft sie sich im Grunde selbst neu auf, was als Rekursion bezeichnet wird. Die notwendige Abbruchbedingung, die dem ganzen ein Ende setzt, wird durch die Wiederholung erreicht. Sie läuft nun mal nur n-Mal und mit jeder neuen Verzweigung wird n um 1 verringert. So hat der Hauptstamm drei Verzweigungen, die ersten Tochterstämme (links und rechts) jeweils zwei Verzweigungen, usw..
Reicht es Dir schon, wenn ich Dir sage, daß der Baum eine rekursive Struktur hat?
Ich muss den baum rechts programmieren , kannst du mir villeicht weiterhelfen?
Okay, anscheinend weißt Du nicht, was eien rekursive Struktur ist. Darf ich fragen: Schule? Welche Jahrgangsstufe?
Wenn Du Dir den 'Baum' anschaust, dann siehst du (vielleicht) eine Selbstähnlichkeit?
\|/
|
Fangen wir mal einfach an Ich habe eine Strecke (Stamm) sowie einen linken, mittleren und rechten Zweig. Und jetzt stelle Dir vor, Du nimmt dieses Gesamtgebilde und verkleinerst es.
Und jetzt ersetzt Du jeden der Zweige durch dieses Gesamtgebilde. Das ist die rekursive Struktur die ich ansprach (bzw. die Selbstähnlichkeit)
Dein 'Baum' ist genau so erzeugt worden, nur daß die Zweige z.B. nicht symmetrisch sind.
Ich gehe recht in der Annahme, daß Dir Lindenmayer-Systeme auch nichts sagen?
Sagt mir leider nichts. Ich bin im Gymnasium in der 8. Jahrgangsstufe. Kannst du mir villeicht ein Programm zeigen, dass so ähnlich aussieht, weil ich noch nie so eine rekursive Struktur programmiert habe.
Jahrgangsstufe 8 - Okay, das wird definitiv nicht einfach, soviel ist sicher.
Immerhin mußt Du Turle nicht selbständig programmieren. Lies Dir auch mal die Antwort von Regex durch. Er beschreibt, wie Du Dich schrittweise an die Lösung annäherst (für Deinen speziellen Fall) und die Rekursion aufbauen kannst.
Versuch das erstmal, dann schauen wir weiter.
Ich weiß nicht wie ich die Funktion und die Rekursion programmieren soll
def paintree(t,l):
if t==0:
fd(l)
else:
fd(l)
lt(20)
painttree(t-1,0.7*l)
Jetzt mußt Du nur die eigentliche Struktur in Form von Turtle-Befehlen im else Zwei einarbeiten und dabei für jeden Zweig einen entsprechenden rekursiven Aufruf angeben.
--------
Eine vollständige Lösung werde ich sicher nicht liefern, das sollte Dir aber als Anhaltspunkt eigentlich ausreichen. Rufe es mal mit gleicher Länge(l) und für unterschiedliceh t(0,1,2, .. auf).
Vielleicht verstehst Du dann das Prinzip der Rekursion.
Die Grundstruktur des Baumes sind ja immer ein Stamm, von dem 3 Zweige absprießen. Diese Zweige sind dann die neuen Stämme, von denen 3 ...
Ich würde also eine Funktion Bauen: draw_stamm(start_xy, end_xy, tiefe)
Und diese Funktion malt den Stamm, wenn tiefe>0 und lässt 3 neue Stämme abzweigend malen (mit tiefe-1).
Erstmal Danke für die Antwort, ich habe die Grundfigur gezeichnet, aber ich weiß nicht wie ich die Funktion und Rekursion programmieren soll