Problem Matheaufgaben (Extremwert)?
Hallo,
ich muss folgende Aufgabe als Hausaufgabe machen, aber ich weiß nicht mal, wie ich anfangen soll, zu rechnen:
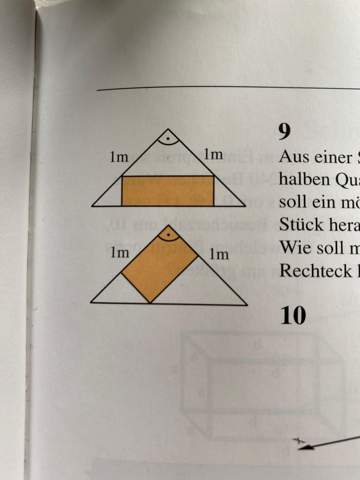
Aus einer Spanplatte von der Form eines halben Quadrates mit der Seitenlänge 1m soll ein möglichst großes rechteckiges Stück herausgesägt werden.
Wie soll man sägen? Wie groß ist das Rechteck höchstens?
Ich erwarte keine vollständigen Lösungen, vielleicht nur einen Ansatz zum Rechnen
Danke im Voraus
.
Die Ausgangsdaten sind irreführend. Was ist ein halbes Quadrat mit einer Seitenlänge von 1m?
ein bild habe ich hochgeladen
2 Antworten
9)
1) ein x-y-Koordinatensystem zeichnen,wo die y-Achse durch den 90° Winkel geht
dadurch wird die Rechteckfläche in 2 gleich große Einzelflächen aufgeteilt
Das Rechteck ist am größten,wenn die halbe Rechteckfläche am größten ist.
2) nun die Funktion der Geraden bestimmen,vom 90° Winkel oben bis unten rechts bei y=f(x)=...=0
Winkel in diesen rechtwinkligen Dreieck Alpha (a)=45° und Beta (b)=45° und Gamma (g)=90°
Steigung der Gerade m=(y2-y1)/(x2-x1)
Punkt P1(0/h) und P2(x/0)
m=(0-h)/(x-0)=-h/x
mit sin(45°)=Gk/Hy=h/1 m → h=sin(45°)*1 m=sin(45°)
cos(45°)=Ak/Hy=x/1 m → x2=cos(45°)*1 m
m=(0-sin(45°))/(cos(45°)-0)=-sin(45°)/cos(45°)=-0,707../0,707..=-1
Funktion der Geraden y=f(x)=-1*x+sin(45°)
1) Ar=a*b ist die Hauptgleichung (Hauptbedingung) Fläche vom halben Rechteck
2) b=f(x)=-1*x+sin(45°)
3) a=x ist die Laufvariable
2) und 3) in 1)
Ar(x)=x*(-1*x+si(45°)=-1*x²+sin(45°)*x
Ar(x)=-1*x²+sin(45°)*x
nun eine Kurvendiskussion durchführen,Extrema bestimmen
A´r(x)=0=-2*x+sin(45°) → x=sin(45°)/2=0,3535..
nun prüfen,ob Maximum oder Minimum
A´´r(x)=-2<0 also ein Maximum
10) hier kannst du das Dreieck so stellen,dass die y-Achse und die x-Achse den 90° Winkel bilden
sin(45°)=Gk/Hy=h/1 m → h=sin(45°)*1 m=sin(45°)
Steigung m=(y2-y1)/(x2-x1) ist hier auch wieder m=-1
aus tan(a)=Gk/Ak=h/x= → tan(45°)=1
1) Ar=a*b → Hauptgleichung
2) b=f(x)=-1*x+sin(45°)
3) a=x
Hier ist allerdings Ar(x)=.. die Gesamtfläche des Rechtecks
Ar(x)=x*(-1*x+sin(45°)
Ar(x)=-1*x²+sin(45°)*x
A´r(x)=0=-2*x+sin(45°)
A´´r(x)=-2<0 → Maximum
Prüfe auf Rechen- und Tippfehler und mach Proberechnungen.
Irgendwas stimmt da nicht.
Eine Spanplatte von der Form eines halben Quadrats mit einer Seitenlänge 1 m → ist eine rechteckige Fläche,soll ein Rechteck ausgeschnitten werden,dessen Fläche möglichst groß ist.
Das ist doch ein Widerspruch.
Mach mal eine Zeichnung,damit man weiß,wei die Verhältnisse sind.
Ist es jetzt verständlicher?