Physik kinetik zug?
Ein Zug fährt mit 72 km/h Geschwindigkeit. Durch eine Baustelle wird er gezwungen, seine Geschwindigkeit auf 18 km/h zu drosseln und kommt deshalb mit 3 min Verspätung am Zielbahnhof an. Die Bremsbeschleunigung ist 0,2 m/s² und die Anfahrbeschleunigung 0,1 m/s².
Wie lang ist die Baustelle? (Aus Sicherheitsgründen hat der Zug am Anfang der Baustelle bereit die kleine Geschwindigkeit und darf erst am Ende wieder beschleunigen)
Hat jemand vielleicht ein Lösungsweg oder könnte mir das errechnen...kriege sie nicht ganz hin...vielen Dank im voraus...
Das Ergebnis basiert auf 4 Abstimmungen
4 Antworten
Die Aufgabe ist unlösbar, denn die Länge des Zuges ist nicht gegeben.
Es wird aber (und so ist es ja auch logisch) expliziet darauf hingewiesen, dass der Zug (die Zugspitze) am Anfang der Baustelle die geringe Geschwindigkeit hat und der Zug (das Zugende) am Ende der Baustelle wieder beschleunigen kann.
Folglich muss der Zug eine Strecke von Zuglänge + Baustellenlänge im geringen Tempo zurücklegen, die Baustellenlänge kann also nur berechnet werden, wenn die Zuglänge bekannt ist.
Stimmt mein Irrtum, Lehrer sind ja bekanntlich unfehlbar....
Stell dir mal folgendes vor, die Baustelle sei gerade mal 1 Millimeter lang. Der Zug selbst sei 1 Kilometer lang.
Für welche Strecke müsste dieser Zug nun langsam fahren?
Die Zugspitze steht am Anfang der Baustelle, der Zug fährt los.
Nach gerade mal 1 mm hat die Zugspitze die Baustelle passiert - jetzt muss die Spitze nur noch 1 Kilometer weiter fahren, damit auch das Ende des Zuges an der Baustelle vorbeigefahren ist.
Obwohl die Baustelle nur 1 mm Lang ist, muss der Zug auf einer Strecke von 1.000.001 Millimeter (1km + 1 mm) die geringe Geschwindigkeit halten.
Wie du siehst, die Länge der Baustelle lässt sich nur dann berechnen, wenn man die Länge des Zuges kennt.
Diese hast du uns entweder nicht in der Aufgabenstellung mitgeteilt - dann hast du den Fehler gemacht.
Oder dein Lehrer hat diese wichtige Größe nicht gegeben, dann hat er den Fehler gemacht.
Den Lösungswegs bis zur Länge auf dem der Zug langsam fährt habe ich dir unter der 2. Frage dazu bereits aufgezeigt
https://www.gutefrage.net/frage/physik-kinetik-zug2#answer-289018000
Zu klären wer den nun was falsch gemacht hat liegt bei dir.
Ja, eigentlich müsste die Länge des Zugs gegeben sein. Oder sie wird stillschweigend vernachlässigt.
Dann dürfte man den Zug als Punkt annehmen, und es würde wohl reichen, wenn
- Die Lok am Anfang der Baustelle auf 5 m/s ist
- und bereits ab Ende der Baustelle wieder beschleunigen darf, so dass halt die letzten Waggons leicht zu schnell durch das Ende der Baustelle fahren.
So würde ich das machen.
Du musst die Fahrt halt komplett zerlegen. Zeichne ein Diagramm. Am Anfang ist 72 km/h konstant, dann bremst er ab, fährt in der Baustelle kontant mit 18 km/h und beschleunigt dann bis er am Ende wieder mit 72 km/h fährt. Das sind 5 Bereiche (s1,s2,s3,s4,s5). Die Geschwindigkeiten solltest du vorher in m/s umrechnen, ebenso die Minuten in Sekunden.
v=s/t => t=s/v (für Bereiche mit konstanter Geschwindigkeit)
v=v0+at (mit dieser Formel berechnest du die Zeit für die Beschleunigung bzw. das Abbremsen)
Mit den berechneten Zeiten kannst du dann die Strecken s2 und s4 berechnen, s = (1/2)at^2+v0t
Gesamt T_b = s1/v0 + s5/v0 + s3/v1 + t2 + t4
Das ist die Zeit mit Baustelle. Die Zeit ohne Baustelle T_ob = s/v0 (s = s1 + s2 + s3 + s4 + s5). v0 wäre hier 72 km/h und v0 wären 18 km/h.
Wir wissen, dass T_ob - T_b = 180s
Wenn du diese Gleichung aufgestellt hast bleibt nur noch s3 als Unbekannte. Nach dieser auflösen und du bist fertig.
Klappt nicht...beziehungsweise kapier ich nicht...+ denke ich eher, dass man das in 3 abschnitte machen muss (Bremsung - fahren - beschleunigung)...will ja nur wissen wie lange die baustelle ist....
Der erste und letzte Abschnitt heben sich in T_ob - T_b so wie so weg.
Vielleicht kannst es einmal Komplet vorrechnen. ^^
Lösung:
Wie groß ist der Weg zum Abbremsen und wie lange braucht der Zug dafür? Der Zug muss 937,5 m vor der Baustelle mit dem Bremsen beginnen. Insgesamt benötigt er für den Brems- und Beschleunigungsvorgang 225 s und legt dabei 2812,5 m zurück.
Wie weit hinter der Baustelle hat er seine ursprüngliche Geschwindigkeit wieder erreicht? 1875m
Insgesamt benötigt er also für den Brems- und Beschleunigungsvorgang 225 s und legt dabei 2812,5 m zurück.
Wie lange hätte er für diese Strecken gebraucht, wenn er nicht gebremst hätte? Er hätte für diese Strecke 140,6 s benötigt. Da er aber für diese Strecke 225 s benötigt hat, hat der durch das Bremsen und Beschleunigen 84,4 s verloren. Das Durchfahren der Baustelle kostet also von den 3 min Verspätung die restlichen 95,6 s.
Die Baustelle ist 637,5 m lang.
Und was bringt ihm die Lösung? Du sollst ihm den Lösungsweg aufzeigen.
Genau Lösungsweg. Den letzten Schritt bei der musterlösung...bzw. allgemein so richtig kapier ich nämlich nicht.
Die Baustelle wäre nur dann 637,5 m lang, wenn der Zug einer Länge von 0 m hätte, was wohl ausgeschlossen werden kann, da es keine Züge dieser Länge gibt ;-)
Diese Aufgabe ist sicher keine Schulaufgabe.
Ich habe nur mal grafisch skizziert, was es zu lösen gilt.
Zudem muss man, weil die Länge des Zugs unbekannt ist, annehmen, dass der Zug sehr kurz ist bzw. die Bedingung nur für den Lokführer gilt, in der Baustelle 5m/s zu fahren. So darf der Zug also bereits wieder beschleunigen, sobald die Lok die Baustelle verlässt. Sonst ist die Aufgabe unlösbar.
Man müsste Bewegungsgleichungen aufstellen, Gleichungssysteme und quadradische Gleichungen lösen.
Ich sehe grad selber nicht durch.
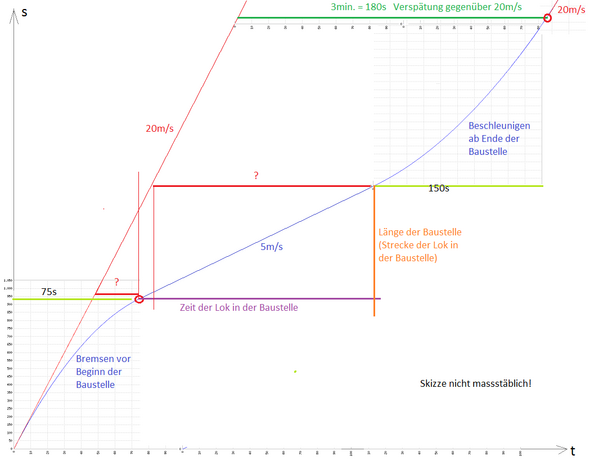
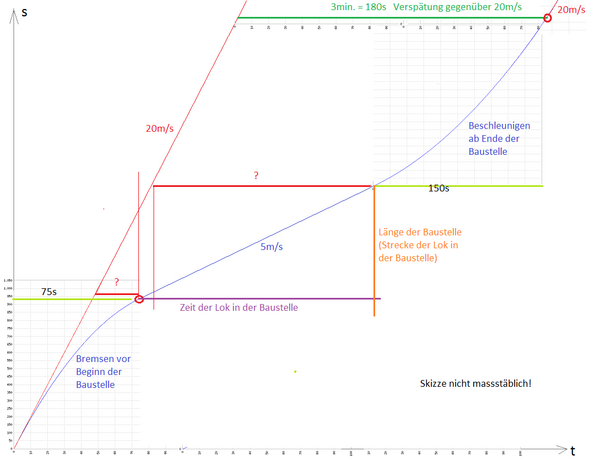
Gleichungssysteme oder quadr. Gleichungen braucht es nicht gleich
siehe zB meinen Lösungsweg hier
https://www.gutefrage.net/frage/physik-kinetik-zug2#answer-289018000
von den Formeln her ist das so gesehen in der Physik der 8. Klasse machbar - allerdings werden von den Schülern nur wenige selbsttätig den Zusammenhang in eine Formel bringen können.
Ich muss ehrlich sagen, dass ich deinen Lösungsweg noch überhaupt nicht durchschaut habe.
Welche Vereinfachungen hast du angenommen?
Ist doch auch erstaunlich, dass sich sonst kein Mathematiker oder Physiker an diese Aufgabe gewagt hat...
Muss lösbar sein, sonst hätte mein Lehrer die nicht als Hausaufgabe angegeben.