Optimierungsaufgabe Schachtel mit Deckel?
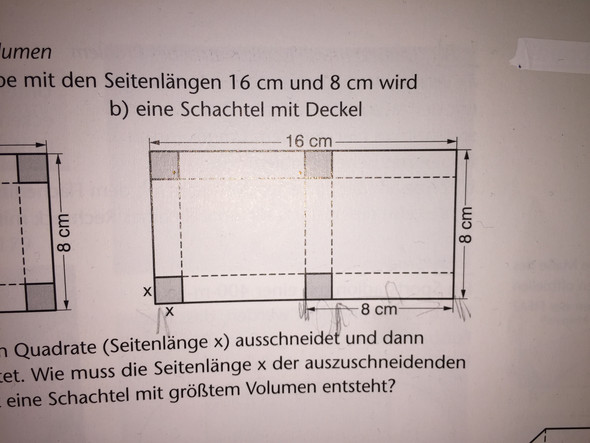
Hallo liebe Community, ich habe ein kleines Problem mit der Mathematik welches sich weder durch das Internet noch durch andere Hilfe für mich lösen lässt. Es geht um folgende Aufgabe: Aus einem rechteckigen Stück Pappe mit den Seitenlängen 16 cm und 8 cm wird eine Schachtel mit Deckel hergestellt, indem man die grauen Quadrate (Seitenlänge x) ausschneidet und dann längs der gestrichelten Linien faltet. Wie muss Seitenlänge x gewählt werden, damit eine Schachtel mit größtem Volumen entsteht? Das Problem ist recht dringlich und ich würde mich wirklich sehr freuen, wenn einer von euch sich die Zeit dafür nehmen würde. Bitte mit Lösungsweg, Danke schon mal im Voraus und einen schönen Sonntag euch Lieben! :) Clara
4 Antworten
In welcher Klasse bist du? Es geht doch um Extremwertaufgaben oder??
Also V = lbh (Volumen gleich Länge mal Breite mal Höhe)
Schau dir das Bild an und Versuch erstmal, dir vorzustellen, wie die Schachtel in 3D aussieht. Die Länge ist 8-x . Die Breite 8-2x und die Höhe x.
Daraus ergibt sich V = (8-x)* (8-2x) * x
= ( 64 - 16x - 8x + 2x^2) *x
= (64 - 24x + 2x^2 ) *x
= 64x -24 x^2 + 2 x^3
Erste Ableitung bilden (Am größten Wert, also größtes Volumen, also Scheitel) ist f'(x) = 0
Also f'(x) = 64 - 48x + 6x^2
Das Gleich Null und mit der Mittelnachsformel auflösen.
Dann, wenn du 2 Werte rausbekommen hast, denn sinnvolleren nehmen, fertig!
Darf ich Fragen welches Buch ihr benutzt? Bzw. welche Jahrgansstufe?
Denn die Aufgaben sind kubische Terme, also eigentlich keine Mittelstufe mehr...
Dann ergibt sich x1 = 6,31 cm
und x2 = 1,7 cm, und da gilt 0 < x < 4 ist x2 die Lösung.
Überleg dir am besten anfangs bei solchen Aufgaben wie man das Volumen berechnet (Grundfläche * Höhe) und welche Variablen einen Einfluss drauf haben. x stellt in diesem Beispiel jeweils die Höhe der Schachtel dar, das du für die Grundfläche von den angegebenen Maßen abziehen musst.
Ich bin in Klasse 10 auf einem G8-Gymnasium in Niedersachen. Unser Buch heißt "Mathematik - Neue Wege".