Oberfläche und Volumen von Zylindern?
Ich Check die Formel von der Oberfläche und dem Volumen eines Zylinders nicht.
Kann's mir jemand anhand der folgenden Textaufgabe erklären? (Nummer 5)
5 Antworten
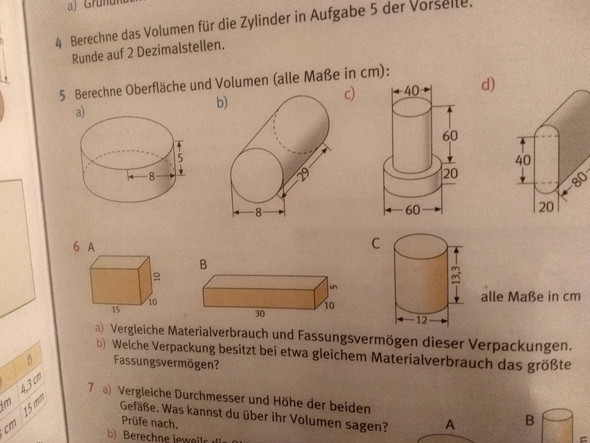
volumen eines zylinders...
stell dir den zylinder als glasbehälter vor, der auf einer seite offen ist... wenn du da wasser hineinfüllst, stellt das wasser das volumen des gesamten zylinders da.
Den Zylinder könntest du nun in einzelen Scheiben, sagen wir in Höhe eines centimeters schneiden... dann wäre die Grundfläche ja gleich, nur die höhe anders...
Bei den centimeterscheiben wäre an jedem Punkt der Grundfläche einen Centimeter hoch wasser... also insgesamt: 1 cm* pi* r^2 (die kreisformel erstmal einfach so hinnehmen, macht es einfacher zu verstehen)
in aufgabe a) hast du einen radius von 8cm, also eine grundfläche von (8*8)* pi - und insgesamt 5 centimeterscheiben - also 8 *1cm*64*pi
Bei der oberfläche stellst du dir wieder einen Behälter vor, aber gehst davon aus, dass das Material biegsam und schneidbar ist... die oberfläche ist der Teil des Behälters, der farbig werden würde, wenn du ihn in einen Farbeimer tauchst...
Zunächst trennst du bei dem Behälter Deckel und Boden ab, das sind zwei normale kreise...
-> also 2* (8*8)*pi
dann hast du noch die seitenfläche... die trennst du mit einen Schnitt auseinander und hast dann ein Rechteck mit der Höhe des Zylinders und der Breite des Umfangs des Kreises (denn: die Seitenfläche war ja um den Kreis gewickelt, daher muss sie genauso breit sein) - formel für ein recheck: breite *höhe
...die höhe ist 5cm
...die Breite, also der Umfang der Grundfläche ist pi*d - also 16*pi
die gesamte Oberfläche ist daher:
...Deckel und boden: 2*(8*8)*pi +
...die seitenfläche: (16*pi)* 5
(ausrechnen musst du es selbst, habe grade keinen taschenrechner da)
bei aufgabe b; genauso...
bei aufgabe c; Zerlege den Körper in zwei Zylinder, der eine ist 20 hoch und hat einen durchmesser von 60, der andere ist 60 hoch und hat einen durchmesser von 40 - die beiden zylinder anschließend zusammenrechnen... Bei der Oberfläche musst du allerdings bedenken, dass der Boden des kleineren (zwei mal!) abgezogen werden muss, denn die berührfläche der beiden zylinder ist ja nicht sichtbar, weder beim großen, noch beim kleinen - und die berührfläche ist der boden des kleinen zylinders...
d; die form zerlegst du in einen quader und zwei halbe zylinder, die du zu einem ganzen zusammenfügst...
bei der oberfläche daran denken, dass du die schmalen seitenflächen des Quaders abziehen musst, die siehst du ja beim ganzen Körper auch nicht.
Schneide ne Dose (ohne Boden) an der Seite auf und mach sie auf dem Tisch platt.... Dann hast du ein Rechteck.... Eine Seite ist der Umfang, andere die Höhe der Dose, plus 2x Fläche eines Deckels
Volumen ist Grundfläche mal Höhe....
Deckelgröße (Kreisfläche) mal Dosenhöhe
sind das deine Formeln für die Oberfläche ?
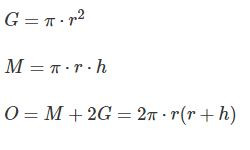
nehmen wir mal c)
2 Zylinder aufeinander
Z - oben und Z - unten ( ZO und ZU )
................
ZU
r = 60/2 = 30
h = 20
Mantel daher
2 * pi * 30 * 20
Bei der Oberfläche kommen noch die beiden Kreise oben und unten dazu ( in der Formel G genannt )
Oberfläche daher
2 * G + M = 2 * ( pi * 30 * 30 ) + M
...................
ZO
selbe Rechnung wie bei ZU
r = 40/2 = 20
h = 60
..............................
Gesamtoberfläche daher ZO + ZU
..............................
Volumen ist einfacher
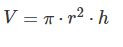
bedenke , daß du die Vs für ZU und ZO getrennt mit unterschiedlichen Höhen und Radien berechnen musst.
.................................
Zur Kontrolle ! der eigenen Rechnungen mit dem TR kann man hier
https://www.schulminator.com/mathematik/zylinder
die Werte eingeben.
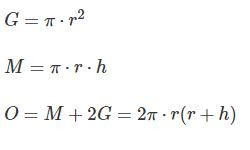
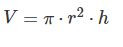
Was meinst du genau mit oberfläche
Die Oberfläche ist die mantelfläche also das um den Zylinder ist + 2* die Grundfläche also Boden + Decke + Rest
Und Volumen ist einfach die Grundfläche mal die Höhe
Eigentlich ist es unmöglich das nicht zu verstehen ein 2d Objekt mal einer Höhe ist ein 3d projekt
Ja die Oberfläche des Zylinders